Fiche 05

Intervenant.e.s

Rédaction

• Clément Poupelin, clementjc.poupelin@gmail.com
  

Relecture

Setup

Packages

# Données
library(dplyr)        # manipulation des données


# Plots
## ggplot
library(ggplot2)
library(gridExtra)

Fonctions

Fonction 1

Fonction 2

Seed

Données

Analyse

Note

METTRE LES REMARQUES

Warning

METTRE LES POINTS D’ATTENTION

Résultats

METTRE LES CONCLUSIONS

Conclusion

Session info

sessioninfo::session_info(pkgs = "attached")

─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.2.1 (2022-06-23 ucrt)
 os       Windows 10 x64 (build 22631)
 system   x86_64, mingw32
 ui       RTerm
 language (EN)
 collate  French_France.utf8
 ctype    French_France.utf8
 tz       Europe/Paris
 date     2025-02-27
 pandoc   3.2 @ C:/Program Files/RStudio/resources/app/bin/quarto/bin/tools/ (via rmarkdown)

─ Packages ───────────────────────────────────────────────────────────────────
 package   * version date (UTC) lib source
 dplyr     * 1.1.4   2023-11-17 [1] CRAN (R 4.2.3)
 ggplot2   * 3.5.1   2024-04-23 [1] CRAN (R 4.2.3)
 gridExtra * 2.3     2017-09-09 [1] CRAN (R 4.2.1)

 [1] C:/Users/cleme/AppData/Local/R/win-library/4.2
 [2] C:/Program Files/R/R-4.2.1/library

──────────────────────────────────────────────────────────────────────────────

EXERCICE 1 :

On considère le modèle AR(2) défini par \[\begin{align} X_t + a_1X_{t-1} + a_2X_{t-2} = \varepsilon_t \end{align}\]

où \((\varepsilon_t)_t\) est une suite iid suivant la loi standard gaussienne.

Pour les trois situations suivantes \[\begin{align} a_1 = \frac{-5}{6} & & a_2 = \frac{1}{6}\\ a_1 = \frac{-5}{6} & & a_2 = 0.9\\ a_1 = -1.12 & & a_2 = 0.5 \end{align}\]

QUESTION 1 : Calculer les racines du polynôme AR

coefs_1 = c(-5/6, 1/6)
coefs_2 = c(-5/6, 0.9)
coefs_3 = c(-1.12, 0.5)

racines_1 = polyroot(c(1,coefs_1))
racines_2 = polyroot(c(1,coefs_2))
racines_3 = polyroot(c(1,coefs_3))

[1] "racines_1 =  2+0i et 3+0i"

[1] "racines_2 =  0.46+0.95i et 0.46-0.95i"

[1] "racines_3 =  1.12+0.86i et 1.12-0.86i"

QUESTION 2 : Tracer la suite des ACF théoriques (ARMAacf)

true_ACF_1 = ARMAacf(ar = (- coefs_1), lag.max = 30)
true_ACF_2 = ARMAacf(ar = (- coefs_2), lag.max = 30)
true_ACF_3 = ARMAacf(ar = (- coefs_3), lag.max = 30)

QUESTION 3 : Simuler et représenter une trajectoire de longueur \(n = 2500\)

n = 2500

trajectoire_1 = arima.sim(list(ar = (-coefs_1)), n)
trajectoire_2 = arima.sim(list(ar = (-coefs_2)), n)
trajectoire_3 = arima.sim(list(ar = (-coefs_3)), n)

QUESTION 4 : A partir de la trajectoire simulée, comparer graphiquement les ACF théoriques et estimées

length(true_ACF_1)

[1] 31

acf(trajectoire_1)
lines(0:30, true_ACF_1, type = "h")

acf(trajectoire_1,col = alpha("blue", 0.5), lwd=2)
lines(0:(length(true_ACF_1)-1), true_ACF_1, type = "h", col = alpha("red", 0.5), lty = 2, lwd = 2)
legend("topright",
       legend = c("ACF empiriques", "ACF théoriques"), 
       col = c("blue","red"),
       lty = c(1,2))

acf(trajectoire_2, col = alpha("blue", 0.5), lwd=2)
lines(0:(length(true_ACF_2)-1), true_ACF_2, type = "h", col = alpha("red", 0.5), lty = 2, lwd = 2)
legend("topright",
       legend = c("ACF empiriques", "ACF théoriques"), 
       col = c("blue","red"),
       lty = c(1,2))

acf(trajectoire_3, col = alpha("blue", 0.5), lwd=2)
lines(0:(length(true_ACF_3)-1), true_ACF_3, type = "h", col = alpha("red", 0.5), lty = 2, lwd = 2)
legend("topright",
       legend = c("ACF empiriques", "ACF théoriques"), 
       col = c("blue","red"),
       lty = c(1,2))

QUESTION 5 : Représenter en fonction de \(n\) l’évolution des estimateurs de \((a_1, a_2)\)

Pour la première trajectoire

n_values = seq(10, 2500, by = 10)

fit_AR2 = function(data, n){
  fit = arima(data[1:n], order = c(2,0,0), include.mean = FALSE, method = "ML")
  #PB pour la trajetoire 2 car non inversible donc rajout method ML
  return(c(-fit$coef[1], -fit$coef[2]))
}


mat1 = matrix(0, ncol = 2, nrow = length(n_values))

for (i in 1:length(n_values)){
  mat1[i,] = fit_AR2(trajectoire_1, n_values[i])
  
}

Pour la deuxième trajectoire

mat2 = matrix(0, ncol = 2, nrow = length(n_values))

for (i in 1:length(n_values)){
  mat2[i,] = fit_AR2(trajectoire_2, n_values[i])
}

Pour la troisième trajectoire

mat3 = matrix(0, ncol = 2, nrow = length(n_values))

for (i in 1:length(n_values)){
  mat3[i,] = fit_AR2(trajectoire_3, n_values[i])
  
}

EXERCICE 2 : Analyse de la série data(lynx)

On note la série \((Ly_t)_t\) . On cherche à modéliser les 109 premières valeurs de cette série par un processus stationnaire AR(p).
Les 5 dernières valeurs sont conservées pour évaluer les performances des prévisions réalisées.

# Importation des données 
data(lynx)
Ly = lynx[1:109]

Modèlisation

QUESTION 1 : Tracer la série \((Ly_t)\), ses autocorrélations empiriques et ses autocorrélations partielles empiriques. Commenter

On peut reconnaitre un porcessus AR avec une acf qui décroit exponentiellement et une pacf qui a un cut off à partir du lag 8.

QUESTION 2 : Modéliser cette série par un processus AR d’ordre \(p\)

On va donc modéliser plusieurs processus avec au maximum \(p=8\). Pour cela on va utiliser la fonction auto.arima

modele_ar = auto.arima(ts(Ly),d=0,D=0,max.p = 8, max.q = 0, max.order = 8, start.p = 8, stationary = TRUE, seasonal = FALSE, ic = "bic", trace = TRUE)

 ARIMA(8,0,0) with non-zero mean : 1816.864
 ARIMA(0,0,0) with non-zero mean : 1926.811
 ARIMA(1,0,0) with non-zero mean : 1853.706
 ARIMA(0,0,0) with zero mean     : 1992.563
 ARIMA(7,0,0) with non-zero mean : 1823.973
 ARIMA(8,0,0) with zero mean     : 1821.505

 Best model: ARIMA(8,0,0) with non-zero mean 

summary(modele_ar)

Series: ts(Ly) 
ARIMA(8,0,0) with non-zero mean 

Coefficients:
         ar1      ar2     ar3      ar4      ar5     ar6      ar7     ar8
      1.0531  -0.6273  0.2099  -0.1429  -0.0198  0.0365  -0.2363  0.3298
s.e.  0.0900   0.1336  0.1461   0.1460   0.1465  0.1455   0.1329  0.0924
           mean
      1549.7982
s.e.   189.4505

sigma^2 = 700446:  log likelihood = -884.98
AIC=1789.95   AICc=1792.2   BIC=1816.86

Training set error measures:
                    ME   RMSE     MAE       MPE     MAPE      MASE        ACF1
Training set -15.39004 801.63 558.127 -45.86168 114.6477 0.6625672 -0.02139499

QUESTION 3 : Peut on valider la modélisation obtenue

Si la modélisation choisie est valide, alors les résidus du modèle doivent former un bruit blanc.
On peut alors regarder si l’ACF empirique et la PACF empirique des résidus sont similaires à celles d’un bruit blanc :

par(mfrow=c(1, 2))
acf(modele_ar[["residuals"]])
pacf(modele_ar[["residuals"]])

par(mfrow=c(1, 1))

Les autocorrélations empiriques suggèrent donc que les résidus forment un bruit blanc.

Il est néanmoins important de vérifier si les paramètres du modèle sont significatifs (surtout le coefficient d’ordre p !!!).

On peut le faire (manuellement) par un test asymptotique de la significativité individuelle des coefficients en comparant par exemple les coefficients standardisés aux quantiles de la loi normale standard (\(\pm 1.96\) pour un test bilatéral au risque \(\alpha = 5\%\)) :

abs(modele_ar[["coef"]] / sqrt(diag(modele_ar[["var.coef"]]))) >= 1.96

      ar1       ar2       ar3       ar4       ar5       ar6       ar7       ar8 
     TRUE      TRUE     FALSE     FALSE     FALSE     FALSE     FALSE      TRUE 
intercept 
     TRUE 

Il est également possible d’utiliser la fonction coeftest de la librairie lmtest :

coeftest(modele_ar)

z test of coefficients:

             Estimate  Std. Error z value  Pr(>|z|)    
ar1          1.053061    0.090009 11.6995 < 2.2e-16 ***
ar2         -0.627343    0.133628 -4.6947 2.670e-06 ***
ar3          0.209905    0.146086  1.4369 0.1507583    
ar4         -0.142866    0.145959 -0.9788 0.3276746    
ar5         -0.019799    0.146459 -0.1352 0.8924675    
ar6          0.036463    0.145479  0.2506 0.8020931    
ar7         -0.236312    0.132936 -1.7776 0.0754641 .  
ar8          0.329843    0.092361  3.5712 0.0003553 ***
intercept 1549.798224  189.450452  8.1805 2.827e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

On peut alors ré-estimer le modèle en fixant les coefficients non significatifs à 0 (ce qui revient à supprimer les variables non significatives dans la régression linéaire multiple : cette étape fait donc partie de la sélection du modèle et non de la validation proprement-dite)

modele_ar_final = Arima(Ly, order = c(8,0,0), include.mean = TRUE, method = c("CSS-ML", "ML", "CSS"),
  fixed = c(NA, NA, 0, 0, 0, 0, 0, NA, NA))

summary(modele_ar_final)

Series: Ly 
ARIMA(8,0,0) with non-zero mean 

Coefficients:
         ar1      ar2  ar3  ar4  ar5  ar6  ar7     ar8       mean
      1.0854  -0.4857    0    0    0    0    0  0.1836  1545.0887
s.e.  0.0737   0.0788    0    0    0    0    0  0.0572   353.1573

sigma^2 = 750280:  log likelihood = -891.11
AIC=1792.21   AICc=1792.8   BIC=1805.67

Training set error measures:
                    ME    RMSE      MAE       MPE     MAPE      MASE
Training set -4.378324 850.145 583.7302 -54.96815 134.3959 0.6929614
                     ACF1
Training set -0.006081288

Les ACF et PACF empiriques des résidus du modèle correspondent à ceux d’un bruit blanc. On peut donc “a priori” valider ce modèle.

(Il faut noter quand même que la variance des résidus sigma^2 est très élevée !!! Une transformation log pourrait être intéressante si nécessaire)

QUESTION 4 : Calculer et représenter les racines du polynôme auto-régressif

# On prend le modèle AR avec coef non significatifs
modele_ar_coef = modele_ar[["coef"]][paste0('ar',1:8)] 

# On calcul les racines 
racines_poly_ar = polyroot(c(1, -modele_ar_coef))

[1]  0.83+0.63i -0.66+0.99i -0.66-0.99i  0.83-0.63i  0.24+1.10i -1.29+0.00i
[7]  0.24-1.10i  1.19+0.00i

[1] " "

[1] "Module de la 1 ière racine :  1.04" "Module de la 2 ième racine :  1.2" 
[3] "Module de la 3 ième racine :  1.2"  "Module de la 4 ième racine :  1.04"
[5] "Module de la 5 ième racine :  1.13" "Module de la 6 ième racine :  1.29"
[7] "Module de la 7 ième racine :  1.13" "Module de la 8 ième racine :  1.19"

# On prend le modèle AR avec coef non significatifs fixés à 0
modele_ar_final_coef = modele_ar_final[["coef"]][paste0('ar',1:8)] 

# On calcul les racines
racines_poly_ar_final = polyroot(c(1, -modele_ar_final_coef))

[1]  0.82+0.68i -0.88+1.09i  0.24-1.22i  0.82-0.68i  0.24+1.22i -1.45+0.00i
[7] -0.88-1.09i  1.10+0.00i

[1] " "

[1] "Module de la 1 ière racine :  1.06" "Module de la 2 ième racine :  1.4" 
[3] "Module de la 3 ième racine :  1.24" "Module de la 4 ième racine :  1.06"
[5] "Module de la 5 ième racine :  1.24" "Module de la 6 ième racine :  1.45"
[7] "Module de la 7 ième racine :  1.4"  "Module de la 8 ième racine :  1.1" 

Toutes les racines sont en dehors du disque unité : le processus estimé est causal

On peut les représenter et voir leurs positions par rapport rapport au cercle unité :

# racines
cm = 1/2.54 # conversion centimètres en pouces
xlim = range(c(-1, 1, Re(racines_poly_ar_final)))
ylim = range(c(-1, 1, Im(racines_poly_ar_final)))
ysize = par("fin")[2]


par(fin=c(ysize, ysize))
plot(racines_poly_ar_final, pch = "*", cex = 2, col = "red",
  xlim = xlim, 
  ylim = ylim,
  main = "Racines du polynôme AR et cercle unité",
  xlab = "axe réel", ylab = "axe imaginaire")

# ajout du cercle unité
x = seq(-1,1, length.out = 100)
y = c(sqrt(1 - x^2), -sqrt(1 - rev(x)^2))
lines(c(x,rev(x)), y, col = "blue")

Comparaison avec une série simulée suivant le modèle estimé

QUESTION 5 : Simuler une trajectoire de longueur 109 suivant le modèle autorégressif obtenu à la question 2)

On simule en tenant compte de la variance des résidus et du fait que le processus estimé est non centré (on sait que intercept = mu * (1 - sum(coef(AR))), où mu désigne la moyenne du processus) :

# On pose nos paramètres
sd = sqrt(modele_ar_final$sigma2)
mu = modele_ar_final[["coef"]][["intercept"]]/sum(c(1, -modele_ar_final_coef))


trajectoire = mu + arima.sim(list(ar = modele_ar_final$model$phi), 109, sd = sd)

trajectoire

Time Series:
Start = 1 
End = 109 
Frequency = 1 
  [1] 6296.894 6679.557 7517.424 7480.679 6551.314 6147.638 6692.894 8395.757
  [9] 7950.002 6221.558 6036.222 6007.872 6154.923 6507.039 6827.196 7304.711
 [17] 6566.729 5385.287 4724.883 5578.211 5501.938 4945.395 4391.066 5026.821
 [25] 5716.665 7523.909 8203.676 6975.930 5543.028 3384.652 2452.578 1139.244
 [33] 2243.897 5343.136 7261.971 8794.179 8299.870 7186.059 6088.399 4111.452
 [41] 3576.965 3331.020 3059.353 4794.482 8082.696 9301.217 8753.599 6960.391
 [49] 5312.231 4005.593 4637.021 4772.347 6730.478 6843.427 7608.774 7902.327
 [57] 5599.462 4734.936 5838.209 6528.383 6841.928 6962.252 6262.182 5794.706
 [65] 6338.485 6879.422 5537.375 4671.717 5274.061 5336.618 6076.776 6466.981
 [73] 7036.544 6730.531 7128.128 8037.532 7304.329 5632.829 4549.681 3936.662
 [81] 5945.391 6912.281 6945.500 7219.632 7198.676 7022.255 6249.562 6297.565
 [89] 6258.140 6865.752 7952.480 9147.047 7776.166 6097.659 4892.835 5424.848
 [97] 6526.786 8240.159 9591.384 9882.140 8663.513 7671.786 7887.016 8765.456
[105] 8309.337 7793.462 7231.463 7266.603 7440.669

On peut déjà remarquer que cette série simulée prend de plus grandes valeurs par rapport aux valeurs prises par rapport à la série lynx. Ce constat peut s’expliquer entre autres par la différence qu’il peut y avoir entre la moyenne théorique mu estimée ci-dessus pour un processus AR(p) stationnaire avec la moyenne théorique d’un processus présentant une tendance saisonnière similaire à celle du processus sous-jacent aux données lynx.

QUESTION 6 : Tracer la série simulée, ses autocorrélations empiriques et ses autocorrélations partielles empiriques. Commenter

A part la taille des valeurs prises par la série simulée déjà évoquées, on voit aussi que l’aspect global de la série n’est pas le même que celui de la série lynx.

En effet, là où la série lynx semble présenter une périodicité d’environ 10 ans, il n’en est pas de même de la série simulée (ce qui est tout à fait normal pour un processus AR).

Son ACF empirique présente une pseudo-période de 8 ans (due aux racines complexes du polynôme AR) et son PACF empirique laisserait penser que c’est un processus AR d’ordre \(p < 8\) et non \(8\) (tout dépend de l’aléa dans les différentes simulations : les résultats ne seront pas forcément les mêmes d’une simulation à une autre, sauf si la graine aléatoire est fixée au préalable), un phénomène probablement dû au nombre faible de données (\(109\) ici) ne permettant pas des estimations assez consistantes des autocorrélations d’ordre supérieur dans ce cas précis (en simulant une série de taille largement plus grande que 109, on obtiendrait le comportement attendu pour la PACF empirique).

Néanmoins, ce constat est un signal d’alerte pour faire attention aux estimations obtenues pour la série lynx : \(109\) ce n’est peut-être pas assez et il faut donc être vigilant quant aux conclusions inférées à partir de la modélisation faite.

Prévision

QUESTION 7 : À partir du modèle estimé, calculer les prévisions \(\hat{L}y_{110}, · · · , \hat{L}y_{114}\). Représenter sur un même graphique les prévisions, les valeurs de la série et l’intervalle de prévision

On peut regarder ce que l’on obtient avec le modèle AR estimé précédemment en terme des performances prédictives en utilisant les dernières valeurs de la série non incluse dans la modélisation

pred = forecast(modele_ar_final, h=5)
print(pred)

    Point Forecast     Lo 80    Hi 80      Lo 95    Hi 95
110       677.5229 -432.5403 1787.586 -1020.1723 2375.218
111      1042.4638 -595.7932 2680.721 -1463.0340 3547.962
112      1583.7922 -225.7879 3393.372 -1183.7217 4351.306
113      2203.8110  377.1790 4030.443  -589.7815 4997.403
114      2496.5023  666.9676 4326.037  -301.5295 5294.534

Ly_test = lynx[110:114]
print(Ly_test)

[1]  662 1000 1590 2657 3396

On peut calculer l’erreur moyenne quadratique des prédictions à l’horizon \(h = 5\) :

MSE_pred = sum((pred$mean - Ly_test)^2)/length(pred$mean)
print(MSE_pred)

[1] 203311.8

La MSE en prédiction est énorme. En regardant les prédictions ponctuelles de près, c’est surtout les deux dernières valeurs qui font exploser la MSE :

print(pred$mean - Ly_test)

Time Series:
Start = 110 
End = 114 
Frequency = 1 
[1]   15.522856   42.463798   -6.207789 -453.189028 -899.497699

N.B. Si on avait conservé le modèle avec plusieurs coefficients non significatifs, les performances prédictives auraient été encore pires avec une MSE davantage grande.

On peut ensuite représenter sur un même graphique les prévisions, les valeurs de la série et l’intervalle de prévision (et pourquoi pas les valeurs passées de la série telles que estimées par le modèle lors de son ajustement : ce dernier point est à faire lors de la validation du modèle normalement).

La fonction autoplot de la librairie ggplot2 fait presque tout le travail en une ligne de code si on lui passé un objet produit par la fonction forecast de la librairie du même nom :

autoplot(pred, main="Prédictions de cinq dernières valeurs de la série lynx", ylab='Nombre de lynx', xlab='Années') + theme_light()

Sinon, on peut aussi faire les choses “à la main” :

Pour conclure, nous pouvons voir que ce modèle est potentiellement adapté à des fins de prévision à très court terme (horizons \(h = 2\) ans ou \(h =3\) ans).

En effet, même si il s’ajuste un peu bien sur ces données lynx (cf. la courbe fitted values ci-dessus) et semble suivre le phénomène périodique de la série, nous savons qu’il est non périodique (AR(8)) et nous avons vu précédemment qu’une série simulée suivant ce modèle ne présentait pas les mêmes structures macroscopiques.

De plus, en simulant une série plus longue, on perd de plus en plus les détails périodiques. D’où les prévisions à long terme qui s’éloigneront davantage de la vraie tendance (saisonnière) sous-jacente au processus générant les données.

Enfin, il est impossible de ne pas noter la surdispersion des intervalles de prévision (les bornes inférieures à 95% et 80% donnent des nombres de lynx négatifs !!!).

EXERCICE 3 : Analyse de la série varve

La série varve, disponible dans la librarie astsa, contient l’enregistrement des dépots sédimentaires (varve glacière) dans le Massachusetts pendant 634 années ( il y a près de 12 000 ans). La série (notée \(x_t\)) montre une certaine non-stationnalité.

QUESTION 1 : Comparer la variance de l’échantillon sur la première moitié et la seconde moitié des données. Commenter

dygraph(varve, main = "Trajectoire de la série varve",  ylab = "X_t", xlab='temps') %>% 
  dyRangeSelector()

var_moitie_1 = var(varve[1:317])
var_moitie_2 = var(varve[318:634])

[1] "Variance de la première moitié :  133.457415667053"

[1] "Variance de la seconde moitié :  594.490438823224"

[1] "Comparaison v2/v1 :  4.45453282496005"

La variance de la seconde moitié de données vaut plus de quatre fois celle de la première moitié. La variance n’est donc pas constante et la série est par conséquent non stationnaire.

QUESTION 2 : On applique la transformation \(y_t = log(x_t)\). Illustrer que cette transformation stabilise la variance de la série. Représenter l’évolution de la variance empirique calculée sur des blocs de longueur \(m\). (utiliser rollapply de la librairie zoo )

# Transformation log 
yt = log(varve)

On compare à nouveau les variances

print(paste("Variance de la première moitié : ", var(yt[1:317])))

[1] "Variance de la première moitié :  0.270721652653357"

print(paste("Variance de la seconde moitié : ", var(yt[318:634])))

[1] "Variance de la seconde moitié :  0.451371011716303"

print(paste("Comparaison v2/v1 : ", var(yt[318:634])/var(yt[1:317])))

[1] "Comparaison v2/v1 :  1.6672881806549"

m = 30
evol_var = rollapplyr(yt, width = m, FUN = var)


dygraph(evol_var, main = paste0("Evolution variance empirique Blocs de longueur m = ", m),
        ylab = "Variance empirique",
        xlab='Blocs') %>% 
  dyRangeSelector()

La variance se stabilise en moyenne autour de 0.2 pour des blocs de longueur \(m=30\)

QUESTION 3 : Tracer les histogrammes de \(x_t\) et \(y_t\). Commenter l’effet de la transformation log sur la loi.

La transformation log rend la loi de \(y_t\) moins asymétrique que celle de \(x_t\)

QUESTION 4 : Représenter les autocorrélations de \(y_t\). Commenter

L’ACF empirique suggère la présence d’une tendance polynomiale dans la dynamique de \(y_t\).

QUESTION 5 : Calculer \(u_t = y_t − y_{t−1}\) et analyser les propriétés de cette séries. La différenciation des données \(y_t\) produit elle une série raisonnablement stationnaire ?

ut = diff(yt)

Visuellement, la série semble stationnaire.

adf.test(ut)

Warning in adf.test(ut): p-value smaller than printed p-value

    Augmented Dickey-Fuller Test

data:  ut
Dickey-Fuller = -11.824, Lag order = 8, p-value = 0.01
alternative hypothesis: stationary

kpss.test(ut)

Warning in kpss.test(ut): p-value greater than printed p-value

    KPSS Test for Level Stationarity

data:  ut
KPSS Level = 0.012671, Truncation lag parameter = 6, p-value = 0.1

En complétant l’analyse visuelle avec des tests de stationnarité au risque \(\alpha = 5\%\), le test ADF rejette la non stationnarité et le test KPSS ne rejette pas la stationnarité.

QUESTION 6 : Représenter les autocorrélations empiriques et les autocorrélations partielles empiriques de la série \((u_t)\) Le modèle MA(1) vous semble-t-il justifié pour modéliser la série \((u_t)\) ?

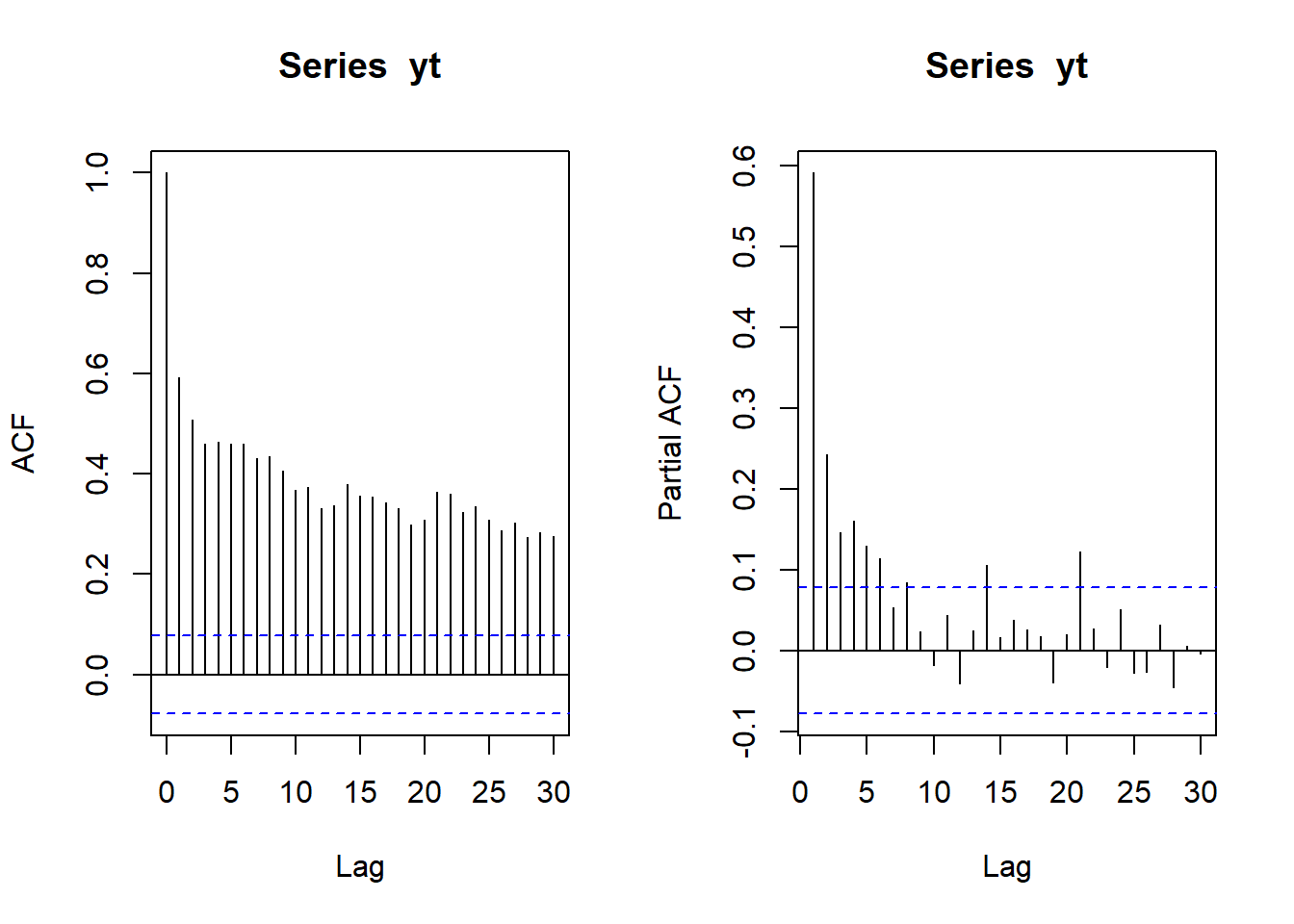
L’ACF empirique suggère que la modélisation MA(1) comme une probable modélisation adéquate sur la série différenciée (et la PACF empirique présente une décroissante exponentielle en valeur absolue avec toutefois des pics atypiques)

QUESTION 7 : Calculer une estimation des paramètres du modèe ARIMA(0,1,1) sur la série \((y_t)\)

modele_0_1_1 = Arima(yt, order = c(0,1,1))
summary(modele_0_1_1)

Series: yt 
ARIMA(0,1,1) 

Coefficients:
          ma1
      -0.7705
s.e.   0.0341

sigma^2 = 0.2357:  log likelihood = -440.72
AIC=885.44   AICc=885.45   BIC=894.34

Training set error measures:
                       ME      RMSE       MAE       MPE     MAPE     MASE
Training set -0.004996908 0.4847107 0.3816333 -2.672511 13.23327 0.842296
                  ACF1
Training set 0.1196371

QUESTION 8 : Peut on valider le modèle estimé sur la série \((y_t)\)

coeftest(modele_0_1_1)

z test of coefficients:

    Estimate Std. Error z value  Pr(>|z|)    
ma1 -0.77054    0.03407 -22.616 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Le coefficient du modèle est significatif. On peut passer à l’analyse des résidus :

Box.test(modele_0_1_1$residuals, lag = 2, fitdf = 1)

    Box-Pierce test

data:  modele_0_1_1$residuals
X-squared = 9.4803, df = 1, p-value = 0.002077

Les ACF et PACF empiriques de résidus du modèle ne correspondent pas à celles d’un bruit blanc ; ce qui est confirmé par le test de portemanteau (ici Box-Pierce) qui rejette l’hypothèse nulle de blancheur (indépendance) des résidus. On ne peut donc pas valider ce modèle.

Si les résidus formaient un bruit blanc, on aurait alors pu vérifier la normalité, hypothèse utilisée souvent pour le calcul des intervalles de prédiction :

hist(modele_0_1_1$residuals, freq = FALSE, col = "skyblue")

shapiro.test(modele_0_1_1$residuals)

    Shapiro-Wilk normality test

data:  modele_0_1_1$residuals
W = 0.99575, p-value = 0.08266

On aurait pu conclure que les résidus sont approximativement gaussiens (histogramme grossièrement semblable à celui d’une gaussienne et le test de Shapiro Wilk ne rejette pas l’hypothèse de normalité au risque 5%)

QUESTION 9 : Si ce modèle n’est pas validé, proposer une autre modélisation ARIMA pour la série \((y_t)\)

On pourrait explorer différents modèles différenciés proches de ARIMA(0,1,1) (par exemple ARIMA(1,1,1) avec et sans drift, etc) et garder celui qui donne des résultats satisfaisants. On peut aussi s’aider de la fonction auto.arima pour faire ces tests de manière automatisée et garder le meilleur modèle suivant le critère d’information de son choix (BIC, AIC, etc)

auto.arima(yt, d=1, stationary = FALSE, seasonal = FALSE, ic = "bic", trace = TRUE)

 Fitting models using approximations to speed things up...

 ARIMA(2,1,2) with drift         : 903.2646
 ARIMA(0,1,0) with drift         : 1111.827
 ARIMA(1,1,0) with drift         : 1010.402
 ARIMA(0,1,1) with drift         : 901.1994
 ARIMA(0,1,0)                    : 1105.379
 ARIMA(1,1,1) with drift         : 889.4259
 ARIMA(2,1,1) with drift         : 898.7784
 ARIMA(1,1,2) with drift         : 894.7764
 ARIMA(0,1,2) with drift         : 891.4283
 ARIMA(2,1,0) with drift         : 979.2122
 ARIMA(1,1,1)                    : 883.1899
 ARIMA(0,1,1)                    : 894.8155
 ARIMA(1,1,0)                    : 1003.956
 ARIMA(2,1,1)                    : 892.6602
 ARIMA(1,1,2)                    : 888.607
 ARIMA(0,1,2)                    : 885.1202
 ARIMA(2,1,0)                    : 972.7741
 ARIMA(2,1,2)                    : 897.1243

 Now re-fitting the best model(s) without approximations...

 ARIMA(1,1,1)                    : 882.2265

 Best model: ARIMA(1,1,1)                    

Series: yt 
ARIMA(1,1,1) 

Coefficients:
         ar1      ma1
      0.2330  -0.8858
s.e.  0.0518   0.0292

sigma^2 = 0.2292:  log likelihood = -431.44
AIC=868.88   AICc=868.91   BIC=882.23

On va ajuster le modèle ARIMA(1,1,1) sans drift (car meilleur modèle au sens du BIC).

On remarque tout de même que notre série non différenciée en possède. On pourrait donc également tester un modèle avec drift.

modele_arima = Arima(yt, order = c(1,1,1), include.drift = FALSE)
summary(modele_arima)

Series: yt 
ARIMA(1,1,1) 

Coefficients:
         ar1      ma1
      0.2330  -0.8858
s.e.  0.0518   0.0292

sigma^2 = 0.2292:  log likelihood = -431.44
AIC=868.88   AICc=868.91   BIC=882.23

Training set error measures:
                       ME      RMSE       MAE       MPE     MAPE      MASE
Training set -0.008779553 0.4775705 0.3754852 -2.824298 13.03097 0.8287266
                     ACF1
Training set -0.008706557

coeftest(modele_arima)

z test of coefficients:

     Estimate Std. Error  z value  Pr(>|z|)    
ar1  0.233002   0.051785   4.4994 6.813e-06 ***
ma1 -0.885763   0.029150 -30.3861 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

On étudit les résidus

Box.test(modele_arima$residuals, lag = 3, fitdf = 2)

    Box-Pierce test

data:  modele_arima$residuals
X-squared = 1.0878, df = 1, p-value = 0.297

shapiro.test(modele_arima$residuals)

    Shapiro-Wilk normality test

data:  modele_arima$residuals
W = 0.99752, p-value = 0.4681

Les résidus satisfont les différents tests non satisfaits précédemment (blancheur) et sont approximativement gaussiens

QUESTION 10 : Pour la modélisation que vous avez retenue (et donc validée ) calculer la prévision aux horizons 1 à 20 avec des intervalles de prévision, pour la série \((y_t)\) puis la série initiale varve

On utilise donc le modèle ARMA(1,1,1) sans drift pour prévoir \(y_t\) et ensuite \(x_t\)

pred_yt = forecast(modele_arima, h = 20)

Pour les prédictions de \(x_t\), il ne faut pas oublier le facteur multiplicatif de correction induit par le passage du log à exp :

pred = pred_yt
pred$mean = exp(pred$mean + pred$model$sigma2/2)
pred$lower = exp(pred$lower)
pred$upper = exp(pred$upper)
pred$fitted = exp(pred$fitted + pred$residuals)
pred$x = exp(pred$x)

On fait une visualisation plus détaillée

Les prévisions sont similaires à celles d’un modèle MA(1) pas adapté à de la prévision à un horizon lointain.