Show the code
# Données
library(dplyr) # manipulation des données
# Esthétique
library(latex2exp) ## TeX
library(ggplot2) ## ggplotClément Poupelin
Invalid Date
March 7, 2025
ggTimeSerie <- function(ts, main_title = NULL) {
df_series <- data.frame(Time = as.numeric(time(ts)), TimeSerie = ts)
colnames(df_series) <- c("Time", "TimeSerie")
if(is.null(main_title)){
main <- latex2exp::TeX(paste0("Série $( x_t )_{t=0, ...,n}$ avec n = ", length(ts)))
} else
main <- latex2exp::TeX(main_title)
p <- ggplot(df_series, aes(x = Time, y = TimeSerie)) +
geom_line(color = "red") +
labs(title = main,
x = "Time",
y = "Simulated series") +
theme_minimal()
if(length(time(ts(ts))) == length(ts)){
p <- p
} else
p <- p +
scale_x_continuous(
breaks = seq(floor(min(df_series$Time)), ceiling(max(df_series$Time)), by = 2),
labels = function(x) floor(x)
)
return(p)
}ggACF <- function(ts) {
acf_data <- acf(ts, plot = FALSE)
df_acf <- data.frame(Lag = acf_data$lag, ACF = acf_data$acf)
pacf_data <- pacf(ts, plot = FALSE)
df_pacf <- data.frame(Lag = pacf_data$lag, PACF = pacf_data$acf)
# Intervalle de confiance
ci <- qnorm((1 + 0.95) / 2) / sqrt(length(ts))
# ACF
p_acf <- ggplot(df_acf, aes(x = Lag, y = ACF)) +
geom_segment(aes(xend = Lag, yend = 0), color = "red") +
geom_point(color = "red") +
labs(title = "Autocorrelation Function (ACF)", x = "Lag", y = "ACF") +
geom_hline(yintercept = c(-ci, ci), color = "blue", linetype = "dashed") +
theme_minimal()
# PACF
p_pacf <- ggplot(df_pacf, aes(x = Lag, y = PACF)) +
geom_segment(aes(xend = Lag, yend = 0), color = "red") +
geom_point(color = "red") +
labs(title = "Partial Autocorrelation Function (PACF)", x = "Lag", y = "PACF") +
geom_hline(yintercept = c(-ci, ci), color = "blue", linetype = "dashed") +
theme_minimal()
return(list(ACF = p_acf, PACF = p_pacf))
}Dans cette exo nous allons travailler sur 3 modèles du type AR(2) avec des coefficient +,+ ou -, - ou +, -.
\(X_t + 1.6X_{t-1} + .64X_{t-2} = w_t\)
\(X_t - .4X_{t-1} - .45X_{t-2} = w_t\)
\(X_t - 1.2X_{t-1} + .85X_{t-2} = w_t\)
n <- 100
a1 <- c(1.6, -0.4, -1.2)
a2 <- c(0.64, -0.45, 0.85)
gridExtra::grid.arrange(
ggTimeSerie(
Sim_AR2(n, a1[1], a2[1]),
main_title = paste0("Série AR(2) avec a1 = ", a1[1], " et a2 = ", a2[1])
),
ggTimeSerie(
Sim_AR2(n, a1[2], a2[2]),
main_title = paste0("Série AR(2) avec a1 = ", a1[2], " et a2 = ", a2[2])
),
ggTimeSerie(
Sim_AR2(n, a1[3], a2[3]),
main_title = paste0("Série AR(2) avec a1 = ", a1[3], " et a2 = ", a2[3])
),
ncol = 3
)
Pour les trois modèles AR(2) décrits ci-dessus, déterminer l’équations de récurrence satisfaite par ACF \(\rho\) et donner la solution (en précisant toutes les constantes)
Nous allons maintenant utiliser les résultats théoriques précédents pour tracer les valeurs des l’ACF \(\rho(h))\) pour \(h = 1...2\). Vérifier vos résultats en utilisant la fonction ARMAacf
─ Session info ───────────────────────────────────────────────────────────────
setting value
version R version 4.4.2 (2024-10-31)
os Ubuntu 24.04.1 LTS
system x86_64, linux-gnu
ui X11
language (EN)
collate fr_FR.UTF-8
ctype fr_FR.UTF-8
tz Europe/Paris
date 2025-03-07
pandoc 3.2 @ /usr/lib/rstudio/resources/app/bin/quarto/bin/tools/x86_64/ (via rmarkdown)
─ Packages ───────────────────────────────────────────────────────────────────
package * version date (UTC) lib source
dplyr * 1.1.4 2023-11-17 [1] CRAN (R 4.4.2)
ggplot2 * 3.5.1 2024-04-23 [1] CRAN (R 4.4.2)
latex2exp * 0.9.6 2022-11-28 [1] CRAN (R 4.4.2)
[1] /home/clement/R/x86_64-pc-linux-gnu-library/4.4
[2] /usr/local/lib/R/site-library
[3] /usr/lib/R/site-library
[4] /usr/lib/R/library
──────────────────────────────────────────────────────────────────────────────Tracer les valeurs des l’ACF \(\rho(h)\) pour \(h = 1, 2\) . Vérifier vos résultats en utilisant la fonction ARMAacf.
0 1 2
1.0000000 -0.9756098 0.9209756 0 1 2
1.0000000 0.7272727 0.7409091 0 1 2
1.00000000 0.64864865 -0.07162162 Pour \(h = 1, 2\) on retrouve bien les valeurs calculées à la question 1.
On se propose de Généraliser en comparant les fonctions calculés en question 1 avec ARMAacf et la fonction acf de r, \(\forall h\).
# On code notre fonction AR(2)
n = 100
AR2 = function(n, a, b) {
eps = rnorm(n + 100)
x = rnorm(n + 100) #c'est pour donner la taille mais après on remplacera toute les valeurs
# on suppose que X_0 est une rnorm
for (i in (3:(n + 100))) {
x[i] = eps[i] - a * x[i - 1] - b * x[i - 2]
}
X_final = x[101:(n + 100)]
return(X_final)
}
# On code des fonction pour définir \rho à partir des calculs de la question 1
rho1 = function(h){
r = (-5/4)^(-h) * (1 + h * (9/41))
return(r)
}
rho2 = function(h){
r = (135/154) * (9/10)^h + (19/154) * (-1)^h * (1/2)^h
return(r)
}
rho3 = function(h){
mod_z1 = sqrt(340/289)
arg_z1 = atan(7/6)
A = ( ( (24/37) * sqrt(30/17) - cos(atan(7/6)) / sin(atan(7/6))) )^2
c1 = -sqrt(1+A)
c2 = acos(1/c1)
r = c1 * mod_z1^(-h) * cos(h * arg_z1 + c2)
return(r)
}





---
title: "Exercice 4.03"
author: "Clément Poupelin"
date: "2025-03-xx"
date-modified: "`r Sys.Date()`"
format:
html:
embed-resources: false
toc: true
code-fold: true
code-summary: "Show the code"
code-tools: true
toc-location: right
page-layout: article
code-overflow: wrap
toc: true
number-sections: false
editor: visual
categories: ["Fiche 4"]
image: ""
description: ""
---
# Intervenant.e.s
### Rédaction
- **Clément Poupelin**, [clementjc.poupelin\@gmail.com](mailto:clementjc.poupelin@gmail.com){.email}\
### Relecture
-
# Setup
:::: panel-tabset
## Packages
```{r, setup, warning=FALSE, message=FALSE}
# Données
library(dplyr) # manipulation des données
# Esthétique
library(latex2exp) ## TeX
library(ggplot2) ## ggplot
```
## Fonctions
::: panel-tabset
### Série temporelle simulée
```{r}
Sim_AR2 <- function(n, a, b) {
eps <- rnorm(n + 100)
x <- rnorm(n + 100)
for (i in (3:(n + 100))) {
x[i] <- eps[i] - a * x[i - 1] - b * x[i - 2]
}
ar2 <- x[101:(n + 100)]
return(ts(ar2))
}
```
### Plot de séries temporelles
```{r}
ggTimeSerie <- function(ts, main_title = NULL) {
df_series <- data.frame(Time = as.numeric(time(ts)), TimeSerie = ts)
colnames(df_series) <- c("Time", "TimeSerie")
if(is.null(main_title)){
main <- latex2exp::TeX(paste0("Série $( x_t )_{t=0, ...,n}$ avec n = ", length(ts)))
} else
main <- latex2exp::TeX(main_title)
p <- ggplot(df_series, aes(x = Time, y = TimeSerie)) +
geom_line(color = "red") +
labs(title = main,
x = "Time",
y = "Simulated series") +
theme_minimal()
if(length(time(ts(ts))) == length(ts)){
p <- p
} else
p <- p +
scale_x_continuous(
breaks = seq(floor(min(df_series$Time)), ceiling(max(df_series$Time)), by = 2),
labels = function(x) floor(x)
)
return(p)
}
```
### Plot pour ACF et PACF
```{r}
ggACF <- function(ts) {
acf_data <- acf(ts, plot = FALSE)
df_acf <- data.frame(Lag = acf_data$lag, ACF = acf_data$acf)
pacf_data <- pacf(ts, plot = FALSE)
df_pacf <- data.frame(Lag = pacf_data$lag, PACF = pacf_data$acf)
# Intervalle de confiance
ci <- qnorm((1 + 0.95) / 2) / sqrt(length(ts))
# ACF
p_acf <- ggplot(df_acf, aes(x = Lag, y = ACF)) +
geom_segment(aes(xend = Lag, yend = 0), color = "red") +
geom_point(color = "red") +
labs(title = "Autocorrelation Function (ACF)", x = "Lag", y = "ACF") +
geom_hline(yintercept = c(-ci, ci), color = "blue", linetype = "dashed") +
theme_minimal()
# PACF
p_pacf <- ggplot(df_pacf, aes(x = Lag, y = PACF)) +
geom_segment(aes(xend = Lag, yend = 0), color = "red") +
geom_point(color = "red") +
labs(title = "Partial Autocorrelation Function (PACF)", x = "Lag", y = "PACF") +
geom_hline(yintercept = c(-ci, ci), color = "blue", linetype = "dashed") +
theme_minimal()
return(list(ACF = p_acf, PACF = p_pacf))
}
```
:::
## Seed
```{r}
set.seed(140400)
```
::::
# Données
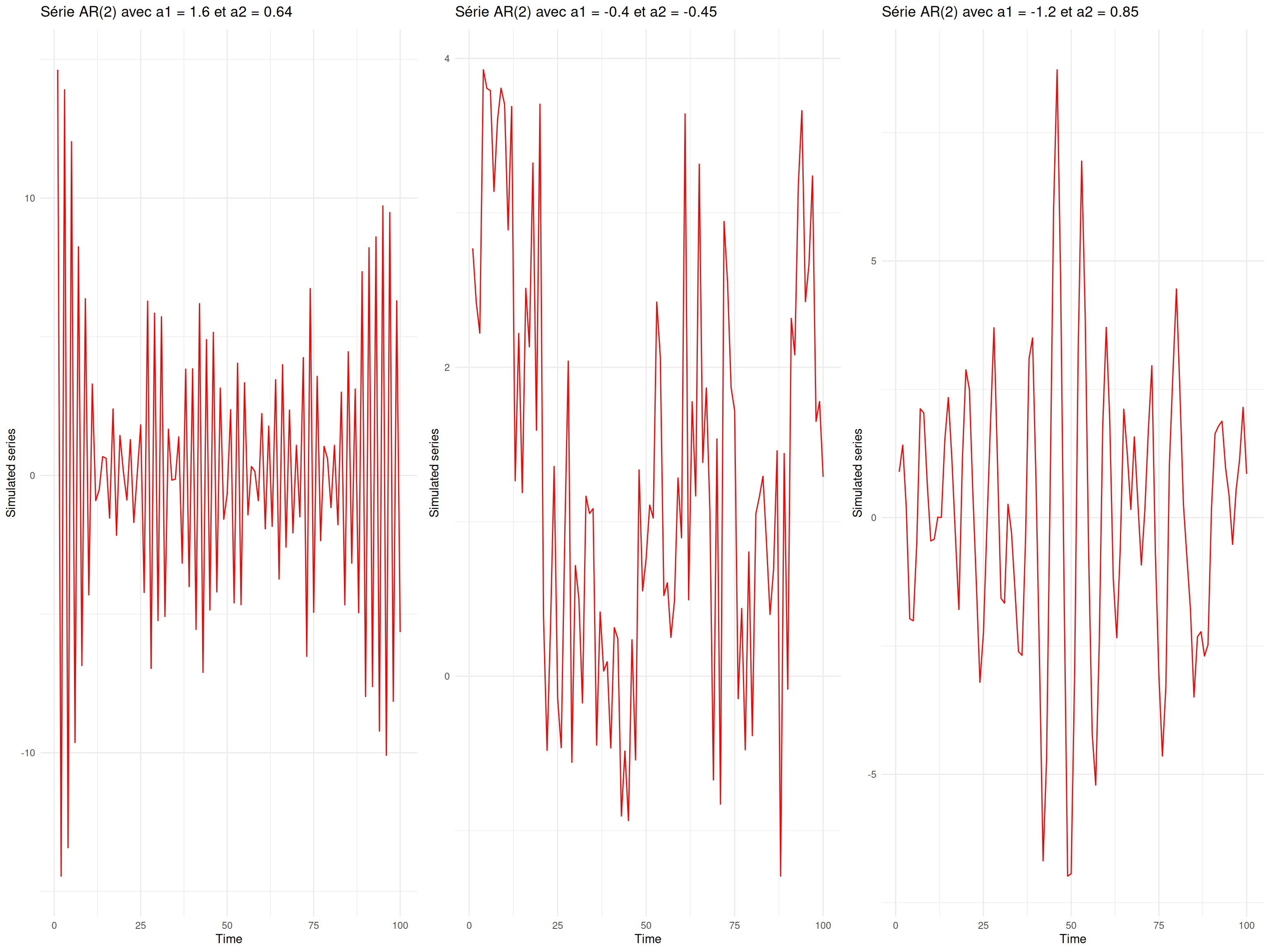
Dans cette exo nous allons travailler sur 3 modèles du type AR(2) avec des coefficient +,+ ou -, - ou +, -.
- $X_t + 1.6X_{t-1} + .64X_{t-2} = w_t$
- $X_t - .4X_{t-1} - .45X_{t-2} = w_t$
- $X_t - 1.2X_{t-1} + .85X_{t-2} = w_t$
```{r, message=FALSE, fig.width=16, fig.height=12}
n <- 100
a1 <- c(1.6, -0.4, -1.2)
a2 <- c(0.64, -0.45, 0.85)
gridExtra::grid.arrange(
ggTimeSerie(
Sim_AR2(n, a1[1], a2[1]),
main_title = paste0("Série AR(2) avec a1 = ", a1[1], " et a2 = ", a2[1])
),
ggTimeSerie(
Sim_AR2(n, a1[2], a2[2]),
main_title = paste0("Série AR(2) avec a1 = ", a1[2], " et a2 = ", a2[2])
),
ggTimeSerie(
Sim_AR2(n, a1[3], a2[3]),
main_title = paste0("Série AR(2) avec a1 = ", a1[3], " et a2 = ", a2[3])
),
ncol = 3
)
```
# Equation de récurrence
Pour les trois modèles AR(2) décrits ci-dessus, déterminer l’équations de récurrence
satisfaite par ACF $\rho$ et donner la solution (en précisant toutes les constantes)
# ACF
Nous allons maintenant utiliser les résultats théoriques précédents pour tracer les valeurs des l’ACF $\rho(h))$ pour $h = 1...2$. Vérifier vos résultats en utilisant la fonction *`ARMAacf`*
# Conclusion
# Session info
```{r}
sessioninfo::session_info(pkgs = "attached")
```
Tracer les valeurs des l’ACF $\rho(h)$ pour $h = 1, 2$ . Vérifier vos résultats en utilisant la fonction **ARMAacf**.
<br>
```{r}
# On pose nos paramètres
a1 = c(1.6, -0.4, -1.2)
a2 = c(0.64, -0.45, 0.85)
```
```{r}
ARMAacf(ar = c(-a1[1], -a2[1]), ma = 0, lag.max = 2, pacf = FALSE)
ARMAacf(ar = c(-a1[2], -a2[2]), ma = 0, lag.max = 2, pacf = FALSE)
ARMAacf(ar = c(-a1[3], -a2[3]), ma = 0, lag.max = 2, pacf = FALSE)
# lag.max = n fait calculer et afficher les n premières valeurs en partant de 0
```
Pour $h = 1, 2$ on retrouve bien les valeurs calculées à la question 1.
#### **BONUS** :
<br>
On se propose de Généraliser en comparant les fonctions calculés en question 1 avec **ARMAacf** et la fonction **acf** de r, $\forall h$.
```{r}
# On code notre fonction AR(2)
n = 100
AR2 = function(n, a, b) {
eps = rnorm(n + 100)
x = rnorm(n + 100) #c'est pour donner la taille mais après on remplacera toute les valeurs
# on suppose que X_0 est une rnorm
for (i in (3:(n + 100))) {
x[i] = eps[i] - a * x[i - 1] - b * x[i - 2]
}
X_final = x[101:(n + 100)]
return(X_final)
}
```
```{r, echo=FALSE}
par(mfrow=c(3, 1))
for (i in 1:3){
plot(ts(AR2(n, a1[i], a2[i])),
main = TeX(paste("$X_t + $",a1[i],"$X_{t-1} +$", a2[i], "$X_{t-2} = w_t$")),
col = "purple",
ylab = "")
mtext(TeX("$X_t$"),
side = 2,
line = 2,
las = 1)
}
par(mfrow=c(1, 1))
```
```{r}
# On code des fonction pour définir \rho à partir des calculs de la question 1
rho1 = function(h){
r = (-5/4)^(-h) * (1 + h * (9/41))
return(r)
}
rho2 = function(h){
r = (135/154) * (9/10)^h + (19/154) * (-1)^h * (1/2)^h
return(r)
}
rho3 = function(h){
mod_z1 = sqrt(340/289)
arg_z1 = atan(7/6)
A = ( ( (24/37) * sqrt(30/17) - cos(atan(7/6)) / sin(atan(7/6))) )^2
c1 = -sqrt(1+A)
c2 = acos(1/c1)
r = c1 * mod_z1^(-h) * cos(h * arg_z1 + c2)
return(r)
}
```
```{r, echo=FALSE}
par(mfrow=c(1, 1))
plot(ts(AR2(n, a1[1], a2[1])),
main = TeX(paste("$X_t + $",a1[1],"$X_{t-1} +$", a2[1], "$X_{t-2} = w_t$")),
col = "purple",
ylab = "")
mtext(TeX("$X_t$"),
side = 2,
line = 2,
las = 1)
par(mfrow=c(1, 3))
t = 0:n
plot(t, rho1(t), col="red", main = TeX("$rho(h)$"), type = "h", ylab = "", xlim = c(0,20))
mtext("ACF",
side = 2,
line = 2,
las = 1)
abline(h = 0)
#abline(h = -0.976, col = "blue") #rho(1)
#abline(h = 0.921, col = "blue") #rho(2)
plot(0:20, ARMAacf(ar = c(-a1[1], -a2[1]), ma = 0, lag.max = 20, pacf = FALSE),
main = "utilisation de ARMAacf", type="h",
xlab="lag",
ylab = "ACF",
col = "red")
abline(h=0)
## ATTENTION AU SIGNE DES COEFF DANS ARMAacf
acf(AR2(n, a1[1], a2[1]),
main = "Fonction ACF de r",
col = "red")
par(mfrow=c(1, 1))
par(mfrow=c(1, 1))
plot(ts(AR2(n, a1[2], a2[2])),
main = TeX(paste("$X_t + $",a1[2],"$X_{t-1} +$", a2[2], "$X_{t-2} = w_t$")),
col = "purple",
ylab = "")
mtext(TeX("$X_t$"),
side = 2,
line = 2,
las = 1)
par(mfrow=c(1, 3))
plot(t, rho2(t), col="red", main = TeX("$rho(h)$"), type = "h", ylab = "", xlim = c(0,20))
mtext("ACF",
side = 2,
line = 2,
las = 1)
abline(h = 0)
plot(0:20, ARMAacf(ar = c(-a1[2], -a2[2]), ma = 0, lag.max = 20, pacf = FALSE),
main = "utilisation de ARMAacf", type="h",
xlab="lag",
ylab = "ACF",
col = "red")
abline(h=0)
## ATTENTION AU SIGNE DES COEFF DANS ARMAacf
acf(AR2(n, a1[2], a2[2]),
main = "Fonction ACF de r",
col = "red")
par(mfrow=c(1, 1))
par(mfrow=c(1, 1))
plot(ts(AR2(n, a1[3], a2[3])),
main = TeX(paste("$X_t + $",a1[3],"$X_{t-1} +$", a2[3], "$X_{t-2} = w_t$")),
col = "purple",
ylab = "")
mtext(TeX("$X_t$"),
side = 2,
line = 2,
las = 1)
par(mfrow=c(1, 3))
plot(t, rho3(t), col="red", main = TeX("$rho(h)$"), type = "h", ylab = "", xlim = c(0,20))
mtext("ACF",
side = 2,
line = 2,
las = 1)
abline(h = 0)
plot(0:20, ARMAacf(ar = c(-a1[3], -a2[3]), ma = 0, lag.max = 20, pacf = FALSE),
main = "utilisation de ARMAacf", type="h",
xlab="lag",
ylab = "ACF",
col = "red")
abline(h=0)
## ATTENTION AU SIGNE DES COEFF DANS ARMAacf
acf(AR2(n, a1[3], a2[3]),
main = "Fonction ACF de r",
col = "red")
par(mfrow=c(1, 1))
```