Intervenant.e.s

Rédaction

Clément Poupelin, clementjc.poupelin@gmail.com

Relecture

Setup

Show the code

# Données
library(dplyr)        # manipulation des données

library(latex2exp)

# Plots
## ggplot
library(ggplot2)
library(gridExtra)

Fonction 1
Fonction 2

Données

Tendance et saisonnalité : étude de la série de vente de voitures. http://www.math.sciences.univ-nantes.fr/~philippe/lecture/voiture.txt

On conserve uniquement le début de la série avant la rupture.

Show the code

url_TP3 = "http://www.math.sciences.univ-nantes.fr/~philippe/lecture/voiture.txt"
X = scan(url_TP3) # pour importer le dataframe en 1 vecteur de donnée (et non un dataframe de dim n*m)

Xt = ts(X, frequency =12)
# On fixe une fréquence de 12

On constate une rupture au niveau du temps 24. On ne conserve donc que la première partie pour notre analyse.

Show the code

Xt = window(Xt, start=start(Xt), end=24)

QUESTION 1 : A l’aide de la suite des covariances empiriques, mettre en évidence la présence d’une tendance et d’une composante saisonnière dans cette série

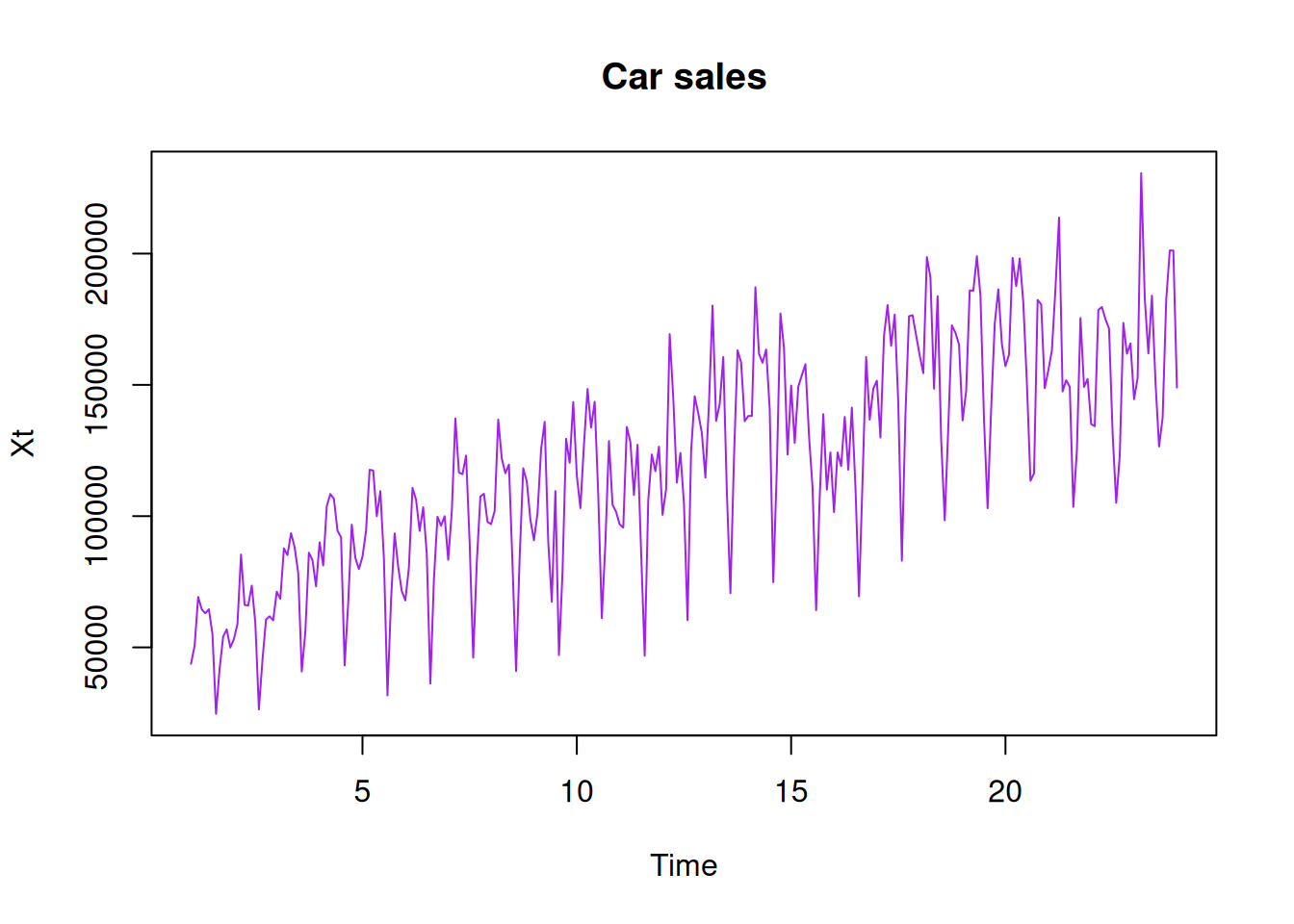
On constate effectivement une tendance globale sur toute la série au vu de nos deux graphes. De plus, l’ACF nous permet de voir une composante saisonnière qui serait probablement de période 12.

Anayse inférentielle

Approche 1
Approche 2

QUESTION 2 : Estimer la tendance et la composante saisonnière de cette série

Pour cette partie, on peut se référé au cours de Séries Temporelle (slides 37-51).

Show the code

#### ETAPE 1 : LISSAGE/FILTRAGE ####

# on suppose période 12 d'après l'acf
d = 12
# si période d pair, filtre :
a = c(1/2,rep(1,d-1),1/2)/d

m = stats::filter(Xt, a, sides = 2)
Z = Xt - m

Le lissage d’une série chronologique (ou le filtrage) est utilisé pour découvrir certaines caractéristiques d’une série temporelle, telles que la tendance et les composantes saisonnières.

Show the code

#### ETAPE 2 : ELIMINATION SAISONNALITE ET TENDANCE ####

# Saisonnalité
Z = ts(Z, frequency = d) # impose la fréquence/période
s.est = 1:12
for ( i in 1:12 ){
  s.est[i]= mean(Z[cycle(Z) == i] , na.rm=TRUE)
}


S.est = ts(rep(s.est,d), frequency = frequency(Xt)) # Saisonnalité estimée

Show the code

# Tendance 

Q = Xt - s.est

Warning in `-.default`(Xt, s.est): la taille d'un objet plus long n'est pas
multiple de la taille d'un objet plus court

Show the code

mod = lm(Q ~ time(Q)) # time(Q) ca fait 1:lenght(Q)
summary(mod)


Call:
lm(formula = Q ~ time(Q))

Residuals:
   Min     1Q Median     3Q    Max 
-51203 -10213   -318   9711  36567 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  57964.5     1882.0   30.80   <2e-16 ***
time(Q)       4958.3      132.9   37.32   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 14730 on 275 degrees of freedom
Multiple R-squared:  0.8351,    Adjusted R-squared:  0.8345 
F-statistic:  1393 on 1 and 275 DF,  p-value: < 2.2e-16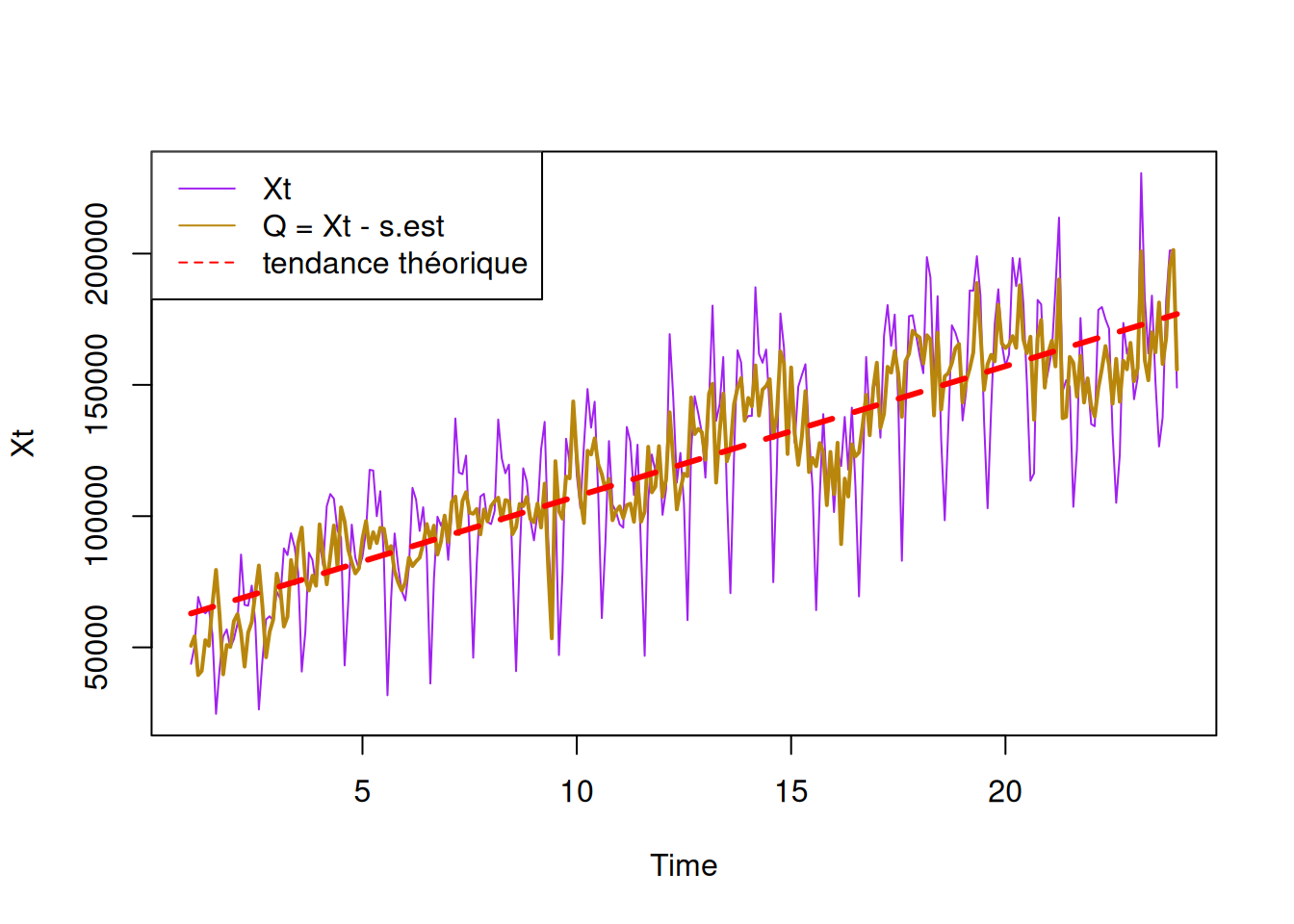

Show the code

P.est = ts(mod$fitted.values, frequency = frequency(Xt)) # Tendance estimée

QUESTION 3 : Éliminer la tendance et la composante saisonnière à partir de vos estimations. On note $(R_j)_j$ la série obtenue

Show the code

Rj = Xt - P.est - S.est

QUESTION 4 : La série $(R_j)_j$ peut elle être modélisée par un bruit blanc ? Discuter le résultat

on a l’impression d’avoir un bruit u peu centré $(E(R_j)=0)$ mais pas dingue avec une variance pas super constante. Mais, avec l’acf, ont voit tout de meme une corrélation faible qui pourrait faire pensé à un BB.

CONCLUSION : ??

Normalité (Test shapiro)

Show the code

shapiro.test(Rj)


    Shapiro-Wilk normality test

data:  Rj
W = 0.98218, p-value = 0.05807

Vérification par le test de Shapiro-Wilk (normalité : p-value > 0,05) On garde l’hypothèse de la normalité

Corrélation

Show the code

cor.test(1:length(Rj), Rj)


    Pearson's product-moment correlation

data:  1:length(Rj) and Rj
t = 2.1745, df = 142, p-value = 0.03133
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.01641902 0.33330168
sample estimates:
      cor 
0.1795128

Les deux valeurs importantes de ce résultat sont la corrélation (50%) et sa p-value (1*10^-8%). Le test nous dit en outre qu’il y a 95% de chances que la “véritable corrélation” entre temps et valeur soit comprise dans “l’intervalle de confiance” entre 36% et 61%. Notez que 0% est un nombre non inclus dans cette fourchette: en d’autres mots, il se pourrait très bien que valeur et temps soient du tout corrélés. En bref, l’algorithme détecte une corrélation.

Le test de la statisticienne finnoise Greta Ljung (et de son directeur de thèse George Box) examine l’autocorrélation d’une série temporelle. Son “hypothèse nulle” est d’avoir affaire à du “bruit blanc”.

Show the code

Box.test(Rj, type="Ljung-Box")


    Box-Ljung test

data:  Rj
X-squared = 26.159, df = 1, p-value = 3.145e-07

La p-value est faible (8e-09). Le test nous permet donc de rejeter l’hypothèse d’avoir affaire à du bruit blanc

QUESTION 5 : Éliminer la tendance et la composante saisonnière en appliquant un ou plusieurs filtres linéaires de la forme $(I − L^s)^d$. On note $(R'_j)_j$ la série obtenue.

Etant donné que l’on a détecter une tendance et une saisonnalité de période 12, on peut tenter une différenciation de la série avec $s=12$ et $d=1$.

Show the code

R1 = diff(Xt, lag=12)

pour enlever le pb en 12, on se propose d’appliquer à nouveau la différence

Show the code

R2 = diff(R1)

QUESTION 6 : La série $(R'_j)_j$ peut elle être modélisée par un bruit blanc ? Discuter le résultat

Conclusion

Session info

Show the code

sessioninfo::session_info(pkgs = "attached")

─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.4.2 (2024-10-31)
 os       Ubuntu 24.04.1 LTS
 system   x86_64, linux-gnu
 ui       X11
 language (EN)
 collate  fr_FR.UTF-8
 ctype    fr_FR.UTF-8
 tz       Europe/Paris
 date     2025-02-28
 pandoc   3.2 @ /usr/lib/rstudio/resources/app/bin/quarto/bin/tools/x86_64/ (via rmarkdown)

─ Packages ───────────────────────────────────────────────────────────────────
 package   * version date (UTC) lib source
 dplyr     * 1.1.4   2023-11-17 [1] CRAN (R 4.4.2)
 ggplot2   * 3.5.1   2024-04-23 [1] CRAN (R 4.4.2)
 gridExtra * 2.3     2017-09-09 [1] CRAN (R 4.4.2)
 latex2exp * 0.9.6   2022-11-28 [1] CRAN (R 4.4.2)

 [1] /home/clement/R/x86_64-pc-linux-gnu-library/4.4
 [2] /usr/local/lib/R/site-library
 [3] /usr/lib/R/site-library
 [4] /usr/lib/R/library

──────────────────────────────────────────────────────────────────────────────

--- title: "Exercie 3.1" author: "Clément Poupelin" date: "2025-02-xx" date-modified: "`r Sys.Date()`" format: html: embed-resources: false toc: true code-fold: true code-summary: "Show the code" code-tools: true toc-location: right page-layout: article code-overflow: wrap toc: true number-sections: false editor: visual categories: ["Fiche 3", "Tendance", "Saisonnalité"] image: "" description: "Nous allons illustrer l'étude de la **tendance** et de la **saisonnalité** à partir d'une base de données sur la vente de voitures" --- # Intervenant.e.s ### Rédaction - **Clément Poupelin**, [clementjc.poupelin\@gmail.com](mailto:clementjc.poupelin@gmail.com){.email}\ ### Relecture - # Setup :::: panel-tabset ## Packages ```{r, setup, warning=FALSE, message=FALSE} # Données library(dplyr) # manipulation des données library(latex2exp) # Plots ## ggplot library(ggplot2) library(gridExtra) ``` ## Fonctions ::: panel-tabset ### Fonction 1 ### Fonction 2 ::: ## Seed :::: # Données **Tendance et saisonnalité** : étude de la série de vente de voitures. http://www.math.sciences.univ-nantes.fr/\~philippe/lecture/voiture.txt On conserve uniquement le début de la série avant la rupture. ```{r} url_TP3 = "http://www.math.sciences.univ-nantes.fr/~philippe/lecture/voiture.txt" X = scan(url_TP3) # pour importer le dataframe en 1 vecteur de donnée (et non un dataframe de dim n*m) Xt = ts(X, frequency =12) # On fixe une fréquence de 12 ``` ```{r, echo=FALSE} plot(Xt, col='purple', main = "Car sales") abline(v=24, lty=2, col='red') legend("topleft", legend = "Rupture", col = "red", lty = "dashed") ``` On constate une rupture au niveau du temps 24. On ne conserve donc que la première partie pour notre analyse. ```{r} Xt = window(Xt, start=start(Xt), end=24) ``` QUESTION 1 : A l’aide de la suite des covariances empiriques, mettre en évidence la présence d’une tendance et d’une composante saisonnière dans cette série ```{r, echo=FALSE} plot(Xt, col='purple', main = "Car sales") par(mfrow=c(1,2)) acf(Xt, col = 'purple', main = TeX("ACF of $X_t$")) pacf(Xt, col = 'purple', main = TeX("PACF of $X_t$")) par(mfrow=c(1,1)) ``` On constate effectivement une tendance globale sur toute la série au vu de nos deux graphes. De plus, l'ACF nous permet de voir une composante saisonnière qui serait probablement de période 12. # Anayse inférentielle ::: panel-tabset ## Approche 1 QUESTION 2 : Estimer la tendance et la composante saisonnière de cette série Pour cette partie, on peut se référé au cours de Séries Temporelle (slides 37-51). ```{r} #### ETAPE 1 : LISSAGE/FILTRAGE #### # on suppose période 12 d'après l'acf d = 12 # si période d pair, filtre : a = c(1/2,rep(1,d-1),1/2)/d m = stats::filter(Xt, a, sides = 2) Z = Xt - m ``` ```{r, echo=FALSE} par(mfrow=c(2, 1)) plot(Xt, col = "purple", main = TeX("Série Temporelle $X_t$ et sa série lissée $m_t$"), ylab = "") mtext(TeX("$X_t$"), side = 2, line = 3, las = 1) lines(m, col = 'darkgreen') legend( "topleft", legend = c(TeX("$X_t$"),TeX( "$m_t$")), col = c("purple", "darkgreen"), lty = c("solid", "solid") ) plot(m, col = "darkgreen", main = TeX("Série lissée $m_t$"), ylab = "") mtext(TeX("$m_t$"), side = 2, line = 3, las = 1) par(mfrow=c(1, 1)) par(mfrow=c(2, 1)) plot(Z, col="blue", main = TeX("$Z = X_t - m_t$"), ylab = "") mtext(TeX("$Z$"), side = 2, line = 3, las = 1) par(mfrow=c(1, 1)) ``` Le lissage d'une série chronologique (ou le filtrage) est utilisé pour découvrir certaines caractéristiques d'une série temporelle, telles que la tendance et les composantes saisonnières. ```{r} #### ETAPE 2 : ELIMINATION SAISONNALITE ET TENDANCE #### # Saisonnalité Z = ts(Z, frequency = d) # impose la fréquence/période s.est = 1:12 for ( i in 1:12 ){ s.est[i]= mean(Z[cycle(Z) == i] , na.rm=TRUE) } S.est = ts(rep(s.est,d), frequency = frequency(Xt)) # Saisonnalité estimée ``` ```{r, echo=FALSE} par(mfrow=c(2, 1)) plot(ts(s.est), col="darkgoldenrod", main = "Estimation de s") plot(ts(rep(ts(s.est), times=400/12)), col="darkgoldenrod", main = "Estimation de s") par(mfrow=c(1, 1)) ``` ```{r} # Tendance Q = Xt - s.est mod = lm(Q ~ time(Q)) # time(Q) ca fait 1:lenght(Q) summary(mod) P.est = ts(mod$fitted.values, frequency = frequency(Xt)) # Tendance estimée ``` ```{r, echo=FALSE} plot(Xt , col = "purple", main ="") lines(Q, col = "darkgoldenrod", main ="Xt - s.est", lwd =2) lines(P.est, col = "red", lty = 2, lwd =3) legend( "topleft", legend = c("Xt", "Q = Xt - s.est", "tendance théorique"), col = c("purple", "darkgoldenrod", "red"), lty = c("solid", "solid", "dashed") ) ``` QUESTION 3 : Éliminer la tendance et la composante saisonnière à partir de vos estimations. On note $(R_j)_j$ la série obtenue ```{r} Rj = Xt - P.est - S.est ``` ```{r, echo=FALSE} par(mfrow=c(2, 1)) plot(Xt, col = "purple", main = "Série Temporelle", ylab = "") mtext(TeX("$X_t$"), side = 2, line = 3, las = 1) plot(P.est, col = "darkolivegreen", main = "Tendance", ylab = "") mtext(TeX(r"($\hat{P}_{est}$)"), side = 2, line = 2, las = 1) par(mfrow=c(1, 1)) par(mfrow=c(2, 1)) plot(S.est, col="darkgoldenrod", main = "Saisonnalité", ylab = "") mtext(TeX(r"($\hat{S}_{est}$)"), side = 2, line = 2, las = 1) plot(Rj, col="hotpink3", main = TeX("$R_j$ résidu"), ylab = "") mtext(TeX("$R_j$"), side = 2, line = 3, las = 1) par(mfrow=c(1, 1)) ``` QUESTION 4 : La série $(R_j)_j$ peut elle être modélisée par un bruit blanc ? Discuter le résultat ```{r, echo=FALSE} plot(Rj, col="hotpink3", main = TeX("$R_j$ résidu"), ylab = "") mtext(TeX("$R_j$"), side = 2, line = 3, las = 1) par(mfrow=c(1, 2)) acf(Rj, col="hotpink3", ylab="") mtext("ACF", side = 2, # (1=bottom, 2=left, 3=top, 4=right) line = 2, las = 1) # rotation pacf(Rj, col="hotpink3", ylab="") mtext("PACF", side = 2, # (1=bottom, 2=left, 3=top, 4=right) line = 2, las = 1) # rotation par(mfrow=c(1, 1)) ``` on a l'impression d'avoir un bruit u peu centré $(E(R_j)=0)$ mais pas dingue avec une variance pas super constante. Mais, avec l'acf, ont voit tout de meme une corrélation faible qui pourrait faire pensé à un BB. CONCLUSION : ?? Normalité (Test shapiro) ```{r} shapiro.test(Rj) ``` Vérification par le test de Shapiro-Wilk (normalité : p-value \> 0,05) On garde l'hypothèse de la normalité Corrélation ```{r} cor.test(1:length(Rj), Rj) ``` Les deux valeurs importantes de ce résultat sont la corrélation (50%) et sa p-value (1\*10\^-8%). Le test nous dit en outre qu’il y a 95% de chances que la “véritable corrélation” entre temps et valeur soit comprise dans “l’intervalle de confiance” entre 36% et 61%. Notez que 0% est un nombre non inclus dans cette fourchette: en d’autres mots, il se pourrait très bien que valeur et temps soient du tout corrélés. En bref, l’algorithme détecte une corrélation. Le test de la statisticienne finnoise Greta Ljung (et de son directeur de thèse George Box) examine l’autocorrélation d’une série temporelle. Son “hypothèse nulle” est d’avoir affaire à du “bruit blanc”. ```{r} Box.test(Rj, type="Ljung-Box") ``` La p-value est faible (8e-09). Le test nous permet donc de rejeter l’hypothèse d’avoir affaire à du bruit blanc ## Approche 2 QUESTION 5 : Éliminer la tendance et la composante saisonnière en appliquant un ou plusieurs filtres linéaires de la forme $(I − L^s)^d$. On note $(R'_j)_j$ la série obtenue. Etant donné que l'on a détecter une tendance et une saisonnalité de période 12, on peut tenter une différenciation de la série avec $s=12$ et $d=1$. ```{r} R1 = diff(Xt, lag=12) ``` ```{r, echo=FALSE} par(mfrow=c(2, 1)) plot(Xt, col = "purple", main = "Série Temporelle", ylab = "") mtext(TeX("$X_t$"), side = 2, line = 3, las = 1) plot(R1, col = "orange", main = "serie diff", ylab = "") mtext(TeX("$R_1$"), side = 2, line = 3, las = 1) par(mfrow=c(1, 1)) par(mfrow=c(3, 1)) plot(R1, col = "orange", main = "serie diff", ylab = "") mtext(TeX("$R_1$"), side = 2, line = 3, las = 1) acf(R1, col = "orange", main = "serie diff") pacf(R1, col = "orange", main = "serie diff") par(mfrow=c(1, 1)) ``` pour enlever le pb en 12, on se propose d'appliquer à nouveau la différence ```{r} R2 = diff(R1) ``` ```{r, echo=FALSE} par(mfrow=c(3, 1)) plot(Xt, col = "purple", main = "Série Temporelle", ylab = "") mtext(TeX("$X_t$"), side = 2, line = 3, las = 1) plot(R1, col = "orange", main = "serie diff", ylab = "") mtext(TeX("$R_1$"), side = 2, line = 3, las = 1) plot(R2, col = "darkorange", main = "serie diff", ylab = "") mtext(TeX("$R_2$"), side = 2, line = 3, las = 1) par(mfrow=c(1, 1)) par(mfrow=c(3, 1)) plot(R2, col = "darkorange", main = "serie diff", ylab = "") mtext(TeX("$R_2$"), side = 2, line = 3, las = 1) acf(R2, col = "darkorange", main = "serie diff") pacf(R2, col = "darkorange", main = "serie diff") par(mfrow=c(1, 1)) ``` QUESTION 6 : La série $(R'_j)_j$ peut elle être modélisée par un bruit blanc ? Discuter le résultat ::: # Conclusion # Session info ```{r} sessioninfo::session_info(pkgs = "attached") ``` ```{r, include=FALSE} # chargement des packages et scripts nécessaires library(latex2exp) library(lmtest) library(dygraphs) ```