Show the code
n = 100
p = 500
X = matrix(rnorm(n*p), n, p)Clément Poupelin
Invalid Date
On souhaite réaliser une petite étude par simulation pour évaluer les qualités respectives de 4 méthodes d’estimation d’un modèle de régression linéaire. On s’intéresse pour chacune d’elle à ses qualités de sélection de variables et à ses qualités prédictives. Le programme SimusReg.R permet de réaliser cette étude. Il contient deux fonctions, Simudata et la fonction principale fun, et un exemple d’utilisation en fin de programme.
Loaded lars 1.3
Attachement du package : 'lars'L'objet suivant est masqué depuis 'package:psych':
error.barsLe chargement a nécessité le package : MatrixLoaded glmnet 4.1-8DataSimulation = function(n,p){
if(p < 4){stop("p>3 require")}
# We create our matrix of explanatory variables
X = matrix(rnorm(n*p), n, p)
# We define our coefficients of regression
coeff = matrix(0, p)
coeff[1:3] = 2
# We build our explanatory variables
y = X%*%coeff + rnorm(n, sd = 2)
return(list(X = X, y = y, coeff = coeff))
}
fun = function(n, p, M = 100){ # By default, we make M = 100 simulation
## Initialization
#################
selec_method1 = NULL; selec_method2 = NULL; selec_method3 = NULL;
taille_method1 = NULL; taille_method2 = NULL; taille_method3 = NULL;
prev_method1 = NULL; prev_method2 = NULL; prev_method3 = NULL; prev_method4 = NULL;
temps1 = NULL; temps2 = NULL; temps3 = NULL; temps4 = NULL;
for(i in 1:M){
cat(paste(i, ":")) # counter to see progress
# We define our train set
datatrain = DataSimulation(n, p)
Xtrain = datatrain$X
y = datatrain$y
coeff = datatrain$coeff
# We define our test set
datatest = DataSimulation(n, p)
Xtest = datatest$X
ytest = datatest$y
## Regression
#################
# Method 1 : Forward-Hybrid with BIC
tic = proc.time()
tab = data.frame(y = y, X = Xtrain)
fit0 = lm(y~1, tab)
fit = lm(y~., tab)
tmp = step(fit0, scope = formula(fit),
k = log(n), # BIC criteria
direction = "both", # Hybrid
trace = 0)
noms = sort(names(tmp$model))
selec_method1[i] = identical(
noms[-length(noms)], sort(paste("X.", which(coeff != 0), sep = ""))
)
taille_method1[i] = length(noms) - 1
prev_method1[i] = mean((predict(tmp,data.frame(X = Xtest)) - ytest)^2)
tac = proc.time() - tic
temps1[i] = tac[3]
# Method 2 : Lasso
tic = proc.time()
cvglm = cv.glmnet(Xtrain, y) # By default we have Lasso
lambda = cvglm$lambda.min
coef2 = coef(cvglm, s = lambda)[-1]
index = which(coef2 != 0)
selec_method2[i] = identical(sort(index), which(coeff != 0))
taille_method2[i] = length(index)
prev_method2[i] = mean((predict(cvglm, Xtest, s = lambda) - ytest)^2)
tac = proc.time() - tic
temps2[i] = tac[3]
# Methods 3 and 4 : Adaptive Lasso and Gauss-Lasso
if(length(index) == 0){
selec_method3[i] = selec_method2[i]
taille_method3[i] = taille_method2[i]
prev_method3[i] = prev_method2[i]
prev_method4[i] = prev_method2[i]}
else{
# Adaptive Lasso part
cvglm = cv.glmnet(Xtrain, y,
penalty.factor = 1/abs(coef2))
lambda = cvglm$lambda.min
coef3 = coef(cvglm, s = lambda)[-1]
index = which(coef3 != 0)
selec_method3[i] = identical(sort(index), which(coeff != 0))
taille_method3[i] = length(index)
prev_method3[i] = mean((predict(cvglm, Xtest, s = lambda) - ytest)^2)
tac = proc.time() - tic
temps3[i] = tac[3]
# Gauss-Lasso part
if(length(index) == 0){
prev_method4[i] = mean((mean(y) - ytest)^2)}
else{
tab = data.frame(y = y, X = Xtrain)
reg = lm(y~.,
data = tab[, c(1, index + 1)])
prev_method4[i] = mean((predict(reg, data.frame(X = Xtest)) - ytest)^2)
tac = proc.time() - tic
temps4[i] = tac[3]
}
}
}
## Results
#################
res = list(mean(selec_method1), mean(selec_method2), mean(selec_method3), taille_method1, taille_method2, taille_method3, prev_method1, prev_method2, prev_method3, prev_method4, mean(temps1), mean(temps2), mean(temps3), mean(temps4))
names(res) = c("selec_method1", "selec_method2", "selec_method3", "taille_method1", "taille_method2", "taille_method3", "prev_method1", "prev_method2", "prev_method3", "prev_method4", "temps1", "temps2", "temps3", "temps4")
return(res)
}
fun2 = function(n, p, M = 100){ # By default, we make M = 100 simulation
## Initialization
#################
selec_method1 = NULL; selec_method2 = NULL; selec_method3 = NULL;
taille_method1 = NULL; taille_method2 = NULL; taille_method3 = NULL;
prev_method1 = NULL; prev_method2 = NULL; prev_method3 = NULL; prev_method4 = NULL;
temps1 = NULL; temps2 = NULL; temps3 = NULL; temps4 = NULL;
for(i in 1:M){
cat(paste(i, ":")) # counter to see progress
# We define our train set
datatrain = DataSimulation(n, p)
Xtrain = datatrain$X
y = datatrain$y
coeff = datatrain$coeff
# We define our test set
datatest = DataSimulation(n, p)
Xtest = datatest$X
ytest = datatest$y
## Regression
#################
# Method 2 : Lasso
tic = proc.time()
cvglm = cv.glmnet(Xtrain, y) # By default we have Lasso
lambda = cvglm$lambda.min
coef2 = coef(cvglm, s = lambda)[-1]
index = which(coef2 != 0)
selec_method2[i] = identical(sort(index), which(coeff != 0))
taille_method2[i] = length(index)
prev_method2[i] = mean((predict(cvglm, Xtest, s = lambda) - ytest)^2)
tac = proc.time() - tic
temps2[i] = tac[3]
# Methods 3 and 4 : Adaptive Lasso and Gauss-Lasso
if(length(index) == 0){
selec_method3[i] = selec_method2[i]
taille_method3[i] = taille_method2[i]
prev_method3[i] = prev_method2[i]
prev_method4[i] = prev_method2[i]}
else{
# Adaptive Lasso part
cvglm = cv.glmnet(Xtrain, y,
penalty.factor = 1/abs(coef2))
lambda = cvglm$lambda.min
coef3 = coef(cvglm, s = lambda)[-1]
index = which(coef3 != 0)
selec_method3[i] = identical(sort(index), which(coeff != 0))
taille_method3[i] = length(index)
prev_method3[i] = mean((predict(cvglm, Xtest, s = lambda) - ytest)^2)
tac = proc.time() - tic
temps3[i] = tac[3]
# Gauss-Lasso part
if(length(index) == 0){
prev_method4[i] = mean((mean(y) - ytest)^2)}
else{
tab = data.frame(y = y, X = Xtrain)
reg = lm(y~.,
data = tab[, c(1, index + 1)])
prev_method4[i] = mean((predict(reg, data.frame(X = Xtest)) - ytest)^2)
tac = proc.time() - tic
temps4[i] = tac[3]
}
}
}
## Results
#################
res = list(mean(selec_method1), mean(selec_method2), mean(selec_method3), taille_method1, taille_method2, taille_method3, prev_method1, prev_method2, prev_method3, prev_method4, mean(temps1), mean(temps2), mean(temps3), mean(temps4))
names(res) = c("selec_method1", "selec_method2", "selec_method3", "taille_method1", "taille_method2", "taille_method3", "prev_method1", "prev_method2", "prev_method3", "prev_method4", "temps1", "temps2", "temps3", "temps4")
return(res)
}1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :[1] 0.9[1] 0.16[1] 0.7 [1] 3 3 4 3 3 3 3 3 3 3 3 3 4 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 3 3 3 3 3
[38] 3 3 4 3 3 3 3 4 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 3 3 3 4 3 3 3 3 3
[75] 3 3 3 3 3 3 3 4 3 3 3 3 3 3 3 3 4 3 3 3 3 3 3 4 3 3 [1] 5 5 5 4 4 5 3 5 3 5 5 5 5 4 4 4 3 4 4 4 5 4 3 4 5 5 4 4 3 5 5 4 4 4 5 4 4
[38] 5 4 5 5 5 5 4 5 5 4 4 5 3 5 4 5 5 5 3 3 4 5 4 4 5 4 3 5 4 5 3 5 4 4 4 5 5
[75] 5 3 4 5 3 4 5 5 5 5 5 5 5 5 3 3 5 5 3 4 5 5 4 4 3 5 [1] 3 3 5 3 3 5 3 3 3 3 3 3 5 3 3 3 3 3 4 3 3 3 3 3 5 3 3 3 3 4 5 4 3 3 4 3 3
[38] 4 3 4 3 3 3 3 5 5 3 3 3 3 3 4 3 4 3 3 3 3 5 3 4 4 3 3 4 3 3 3 4 4 3 3 3 4
[75] 4 3 3 4 3 3 3 5 3 4 3 3 4 3 3 3 5 4 3 3 3 3 3 4 3 3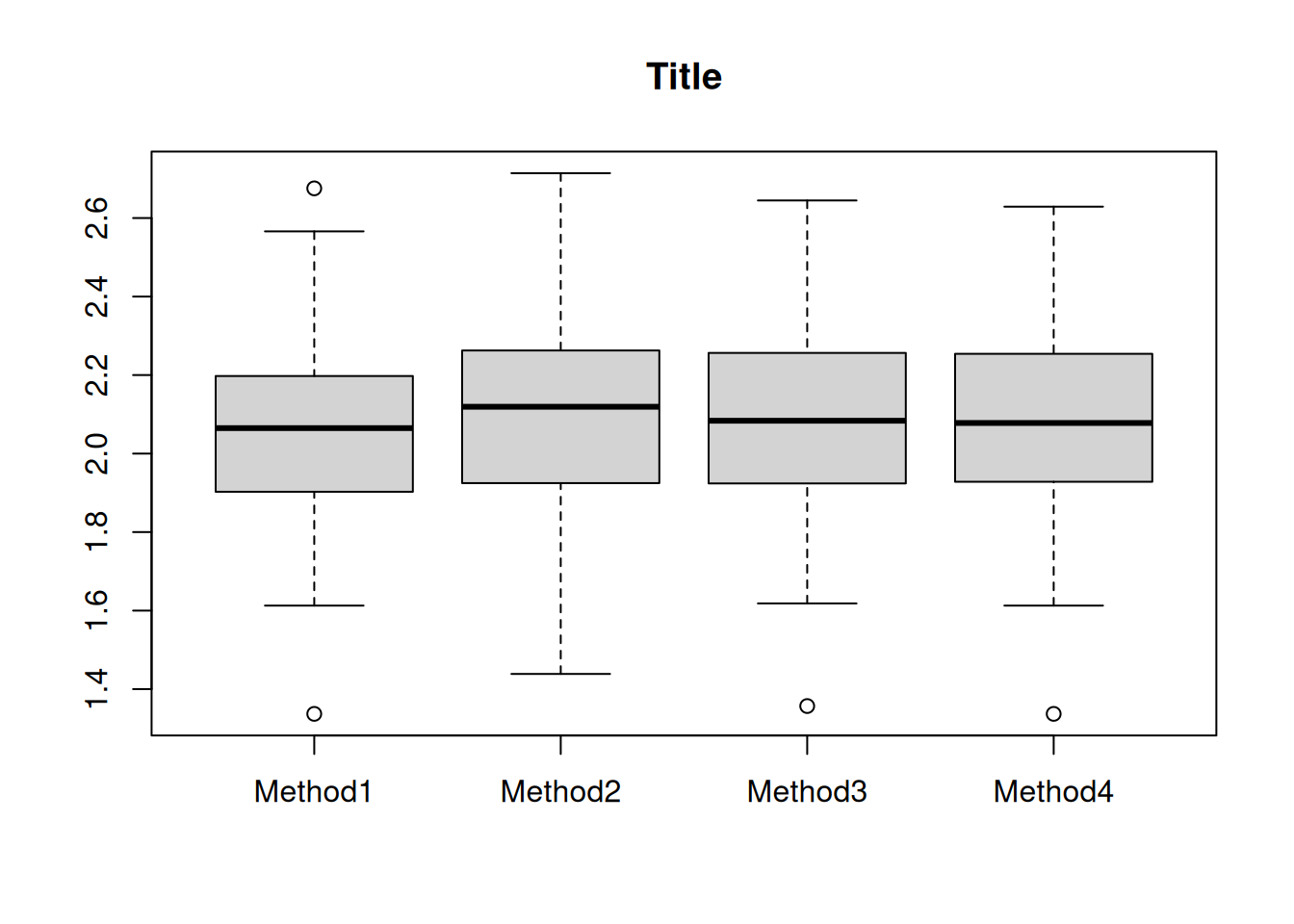
[1] 4.317454[1] 4.482734[1] 4.405399[1] 4.397463[1] 0.01149[1] 0.02251[1] 0.04536[1] 0.04648Quel modèle génère la fonction Simudata ? Combien de variables explicatives sont générées ? Parmi elles, lesquelles sont pertinentes pour la modélisation ? Ecrire l’équation du modèle.
Identifier les 4 méthodes d’estimation mises en oeuvre dans la fonction fun.
Détailler les différentes sorties proposées par la fonction fun.
Remplacer la valeur des options names et title du boxplot réalisé dans l’exemple par les bonnes informations.
Réaliser une étude comparative des méthodes lorsque \(n = 50\) et \(p = n/10\), \(p = n\), \(p = 2n\), \(p = 10n\). Pour chaque situation, on considèrera \(100\) simulations afin de calculer les différents critères. On synthétisera les résultats en terme de qualité de sélection, nombre de variables sélectionnées, erreurs de prévision et temps de calcul.
1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :1 :1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :res_cas1 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas1$selec_method1,r_cas1$selec_method2,r_cas1$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas1$taille_method1),mean(r_cas1$taille_method2),mean(r_cas1$taille_method3),NA),
Prevision_error = c(mean(r_cas1$prev_method1),mean(r_cas1$prev_method2),mean(r_cas1$prev_method3),mean(r_cas1$prev_method4)),
Running_time = c(r_cas1$temps1,r_cas1$temps2,r_cas1$temps3,r_cas1$temps4)
)
t(res_cas1) [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection "0.95" "0.24" "0.76" NA
Mean_nb_selected_var "3.05" "4.19" "3.29" NA
Prevision_error "4.267999" "4.372448" "4.311278" "4.298561"
Running_time "0.01006" "0.02122" "0.04285" "0.04382" boxplot(sqrt(r_cas1$prev_method1),sqrt(r_cas1$prev_method2),sqrt(r_cas1$prev_method3),sqrt(r_cas1$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[1]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))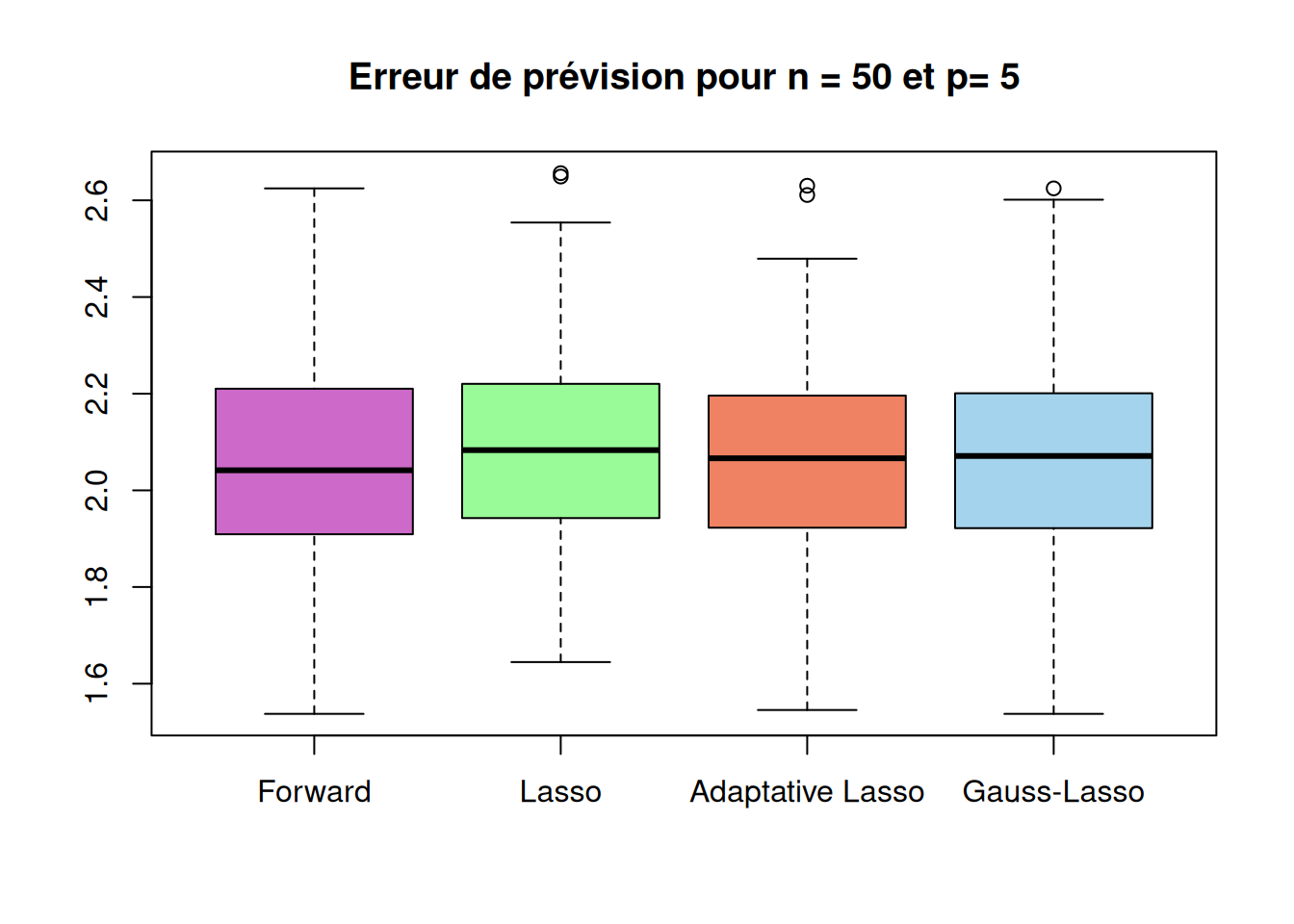
res_cas2 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas2$selec_method1,r_cas2$selec_method2,r_cas2$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas2$taille_method1),mean(r_cas2$taille_method2),mean(r_cas2$taille_method3),NA),
Prevision_error = c(mean(r_cas2$prev_method1),mean(r_cas2$prev_method2),mean(r_cas2$prev_method3),mean(r_cas2$prev_method4)),
Running_time = c(r_cas2$temps1,r_cas2$temps2,r_cas2$temps3,r_cas2$temps4)
)
t(res_cas2) [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection "0.06" "0.01" "0.09" NA
Mean_nb_selected_var " 7.92" "12.88" " 8.17" NA
Prevision_error "7.050225" "5.609938" "5.487207" "6.401796"
Running_time "0.07149" "0.04010" "0.06590" "0.06738" boxplot(sqrt(r_cas2$prev_method1),sqrt(r_cas2$prev_method2),sqrt(r_cas2$prev_method3),sqrt(r_cas2$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[2]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))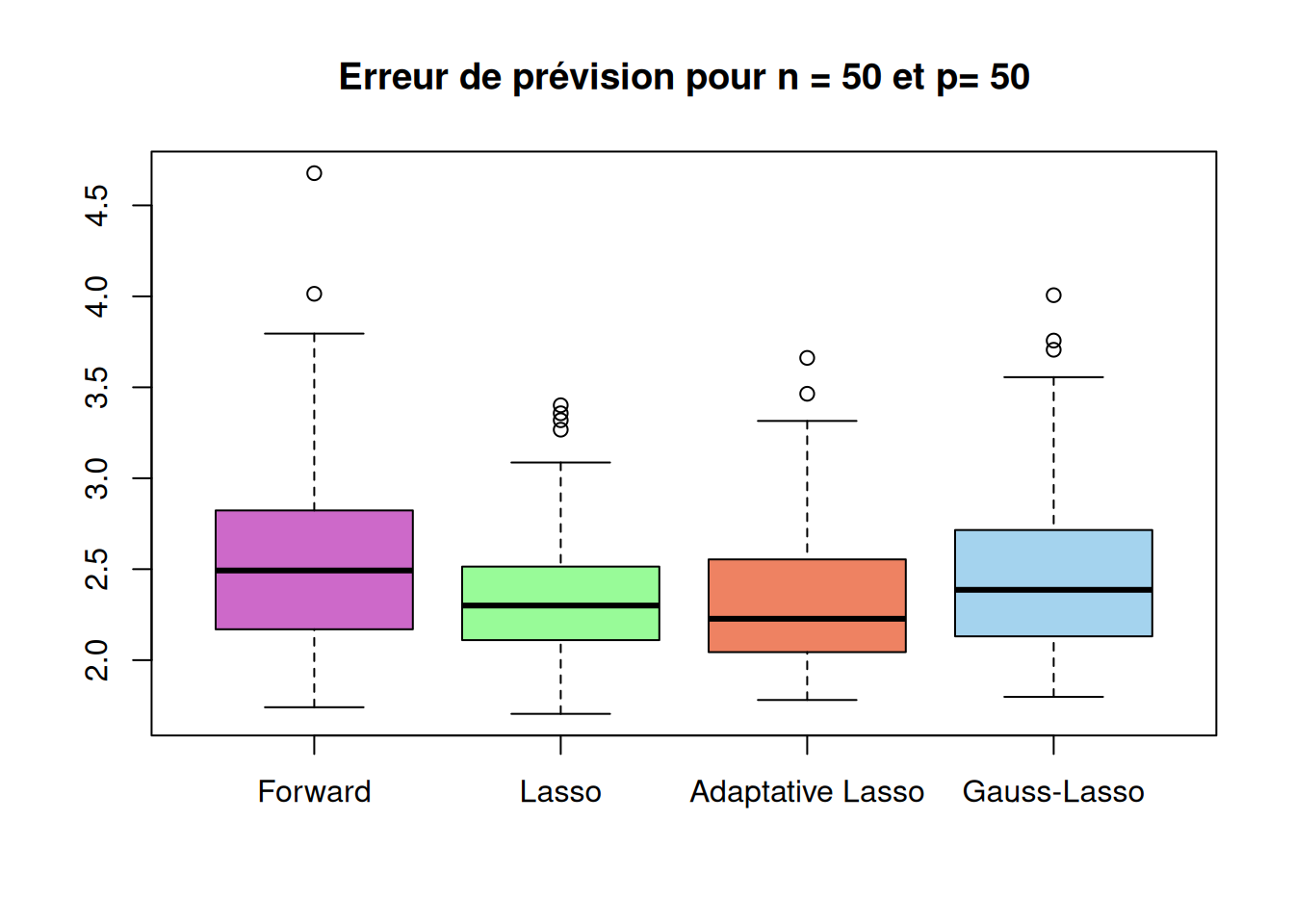
res_cas3 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas3$selec_method1,r_cas3$selec_method2,r_cas3$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas3$taille_method1),mean(r_cas3$taille_method2),mean(r_cas3$taille_method3),NA),
Prevision_error = c(mean(r_cas3$prev_method1),mean(r_cas3$prev_method2),mean(r_cas3$prev_method3),mean(r_cas3$prev_method4)),
Running_time = c(r_cas3$temps1,r_cas3$temps2,r_cas3$temps3,r_cas3$temps4)
)
t(res_cas3) [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection "0.00" "0.00" "0.06" NA
Mean_nb_selected_var "40.57" "15.80" " 9.09" NA
Prevision_error "16.207790" " 6.138163" " 5.738140" " 6.723044"
Running_time "0.71804" "0.04013" "0.06882" "0.07045" boxplot(sqrt(r_cas3$prev_method1),sqrt(r_cas3$prev_method2),sqrt(r_cas3$prev_method3),sqrt(r_cas3$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[3]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))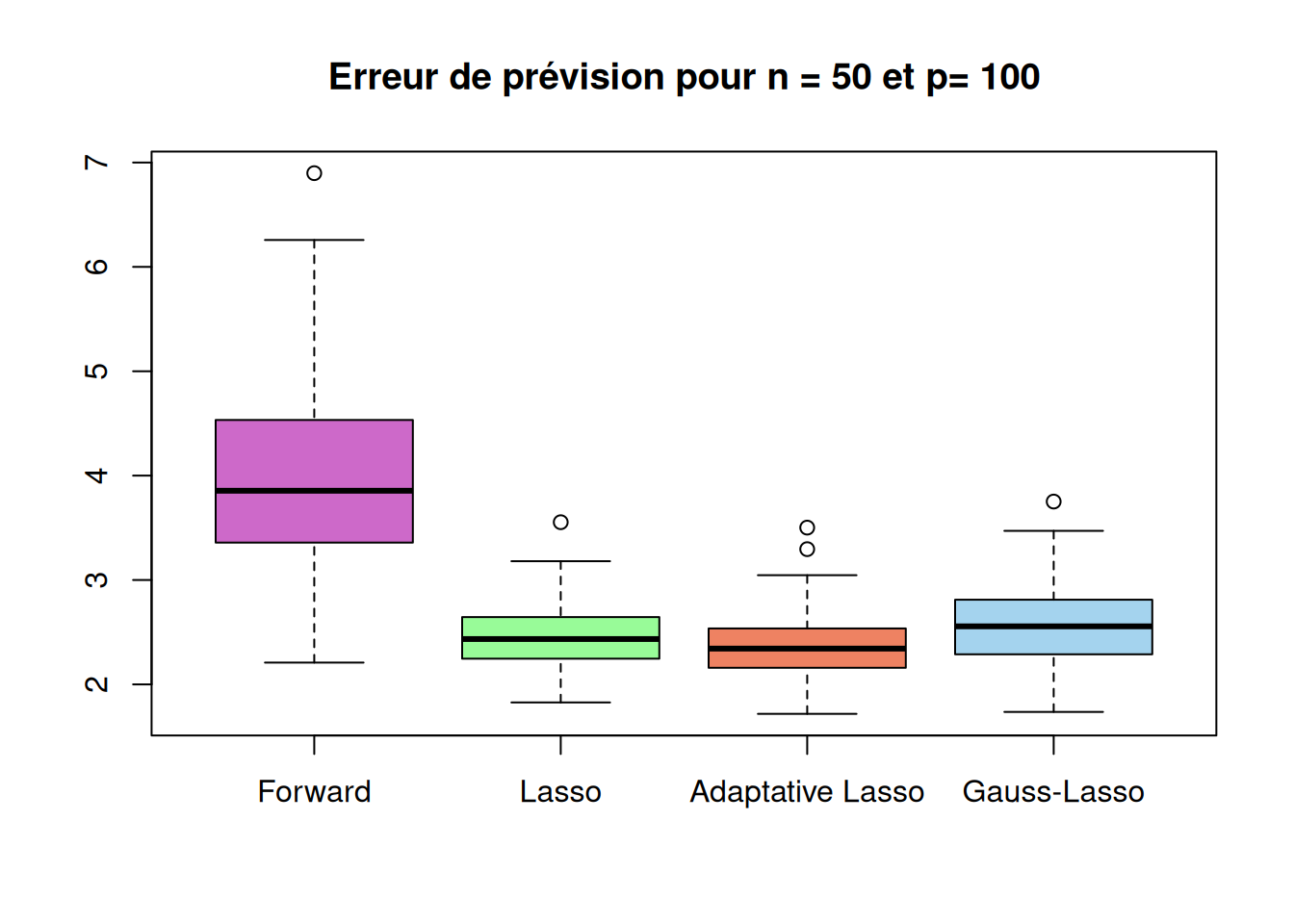
res_cas4 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas4$selec_method1,r_cas4$selec_method2,r_cas4$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas4$taille_method1),mean(r_cas4$taille_method2),mean(r_cas4$taille_method3),NA),
Prevision_error = c(mean(r_cas4$prev_method1),mean(r_cas4$prev_method2),mean(r_cas4$prev_method3),mean(r_cas4$prev_method4)),
Running_time = c(r_cas4$temps1,r_cas4$temps2,r_cas4$temps3,r_cas4$temps4)
)
t(res_cas4) [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection " 0" " 0" " 0" NA
Mean_nb_selected_var "49" "41" "19" NA
Prevision_error "11.762266" " 4.734249" " 4.562205" " 5.403622"
Running_time "6.500" "0.041" "0.077" "0.080" boxplot(sqrt(r_cas4$prev_method1),sqrt(r_cas4$prev_method2),sqrt(r_cas4$prev_method3),sqrt(r_cas4$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[3]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))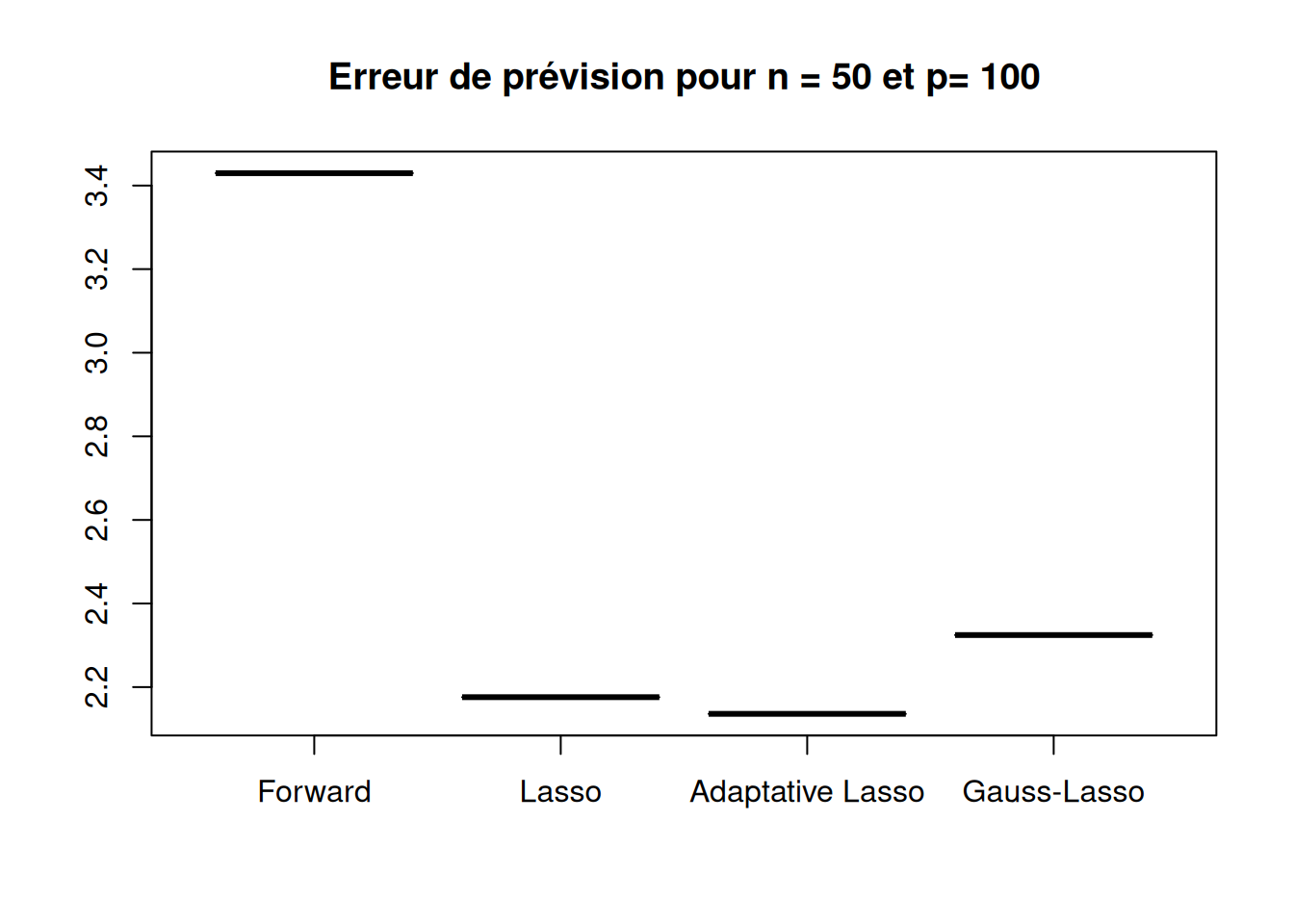
res_cas4bis = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas4bis$selec_method1,r_cas4bis$selec_method2,r_cas4bis$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas4bis$taille_method1),mean(r_cas4bis$taille_method2),mean(r_cas4bis$taille_method3),NA),
Prevision_error = c(mean(r_cas4bis$prev_method1),mean(r_cas4bis$prev_method2),mean(r_cas4bis$prev_method3),mean(r_cas4bis$prev_method4)),
Running_time = c(r_cas4bis$temps1,r_cas4bis$temps2,r_cas4bis$temps3,r_cas4bis$temps4)
)Warning in mean.default(r_cas4bis$taille_method1): l'argument n'est ni
numérique, ni logique : renvoi de NAWarning in mean.default(r_cas4bis$prev_method1): l'argument n'est ni numérique,
ni logique : renvoi de NA [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection NA "0.00" "0.04" NA
Mean_nb_selected_var NA "24.87" "12.34" NA
Prevision_error NA "7.230664" "6.781834" "7.861071"
Running_time NA "0.04820" "0.08404" "0.08697" boxplot(sqrt(r_cas4$prev_method1),sqrt(r_cas4bis$prev_method2),sqrt(r_cas4bis$prev_method3),sqrt(r_cas4bis$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[4]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))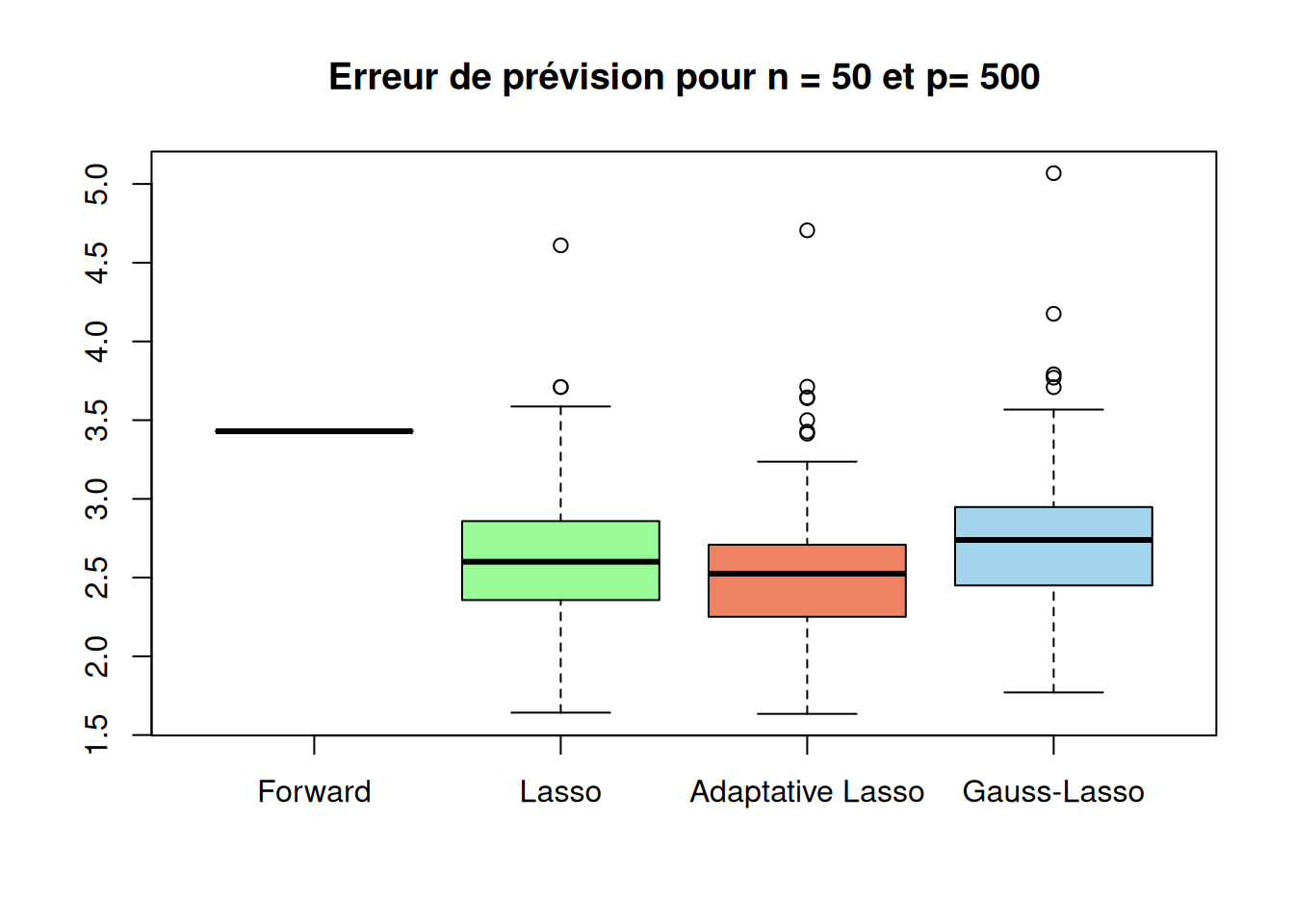
Réaliser la même étude pour \(n = 100\) et \(p = n/10\), \(p = n\), \(p = 2n\), toujours basée sur \(100\) simulations dans chaque cas. Considérer de plus le cas \(p = 10n\) en ne faisant qu’une seule simulation afin d’en évaluer le temps de calcul. Une fois ce temps analysé, lancer \(100\) simulations pour \(p = 10n\) mais en omettant la méthode la plus couteuse en temps de calcul.
1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :1 :1 :2 :3 :4 :5 :6 :7 :8 :9 :10 :11 :12 :13 :14 :15 :16 :17 :18 :19 :20 :21 :22 :23 :24 :25 :26 :27 :28 :29 :30 :31 :32 :33 :34 :35 :36 :37 :38 :39 :40 :41 :42 :43 :44 :45 :46 :47 :48 :49 :50 :51 :52 :53 :54 :55 :56 :57 :58 :59 :60 :61 :62 :63 :64 :65 :66 :67 :68 :69 :70 :71 :72 :73 :74 :75 :76 :77 :78 :79 :80 :81 :82 :83 :84 :85 :86 :87 :88 :89 :90 :91 :92 :93 :94 :95 :96 :97 :98 :99 :100 :res_cas1 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas1$selec_method1,r_cas1$selec_method2,r_cas1$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas1$taille_method1),mean(r_cas1$taille_method2),mean(r_cas1$taille_method3),NA),
Prevision_error = c(mean(r_cas1$prev_method1),mean(r_cas1$prev_method2),mean(r_cas1$prev_method3),mean(r_cas1$prev_method4)),
Running_time = c(r_cas1$temps1,r_cas1$temps2,r_cas1$temps3,r_cas1$temps4)
)
t(res_cas1) [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection "0.71" "0.08" "0.42" NA
Mean_nb_selected_var "3.30" "6.35" "4.15" NA
Prevision_error "4.270127" "4.367182" "4.300236" "4.347811"
Running_time "0.01367" "0.02255" "0.04586" "0.04690" boxplot(sqrt(r_cas1$prev_method1),sqrt(r_cas1$prev_method2),sqrt(r_cas1$prev_method3),sqrt(r_cas1$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[1]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))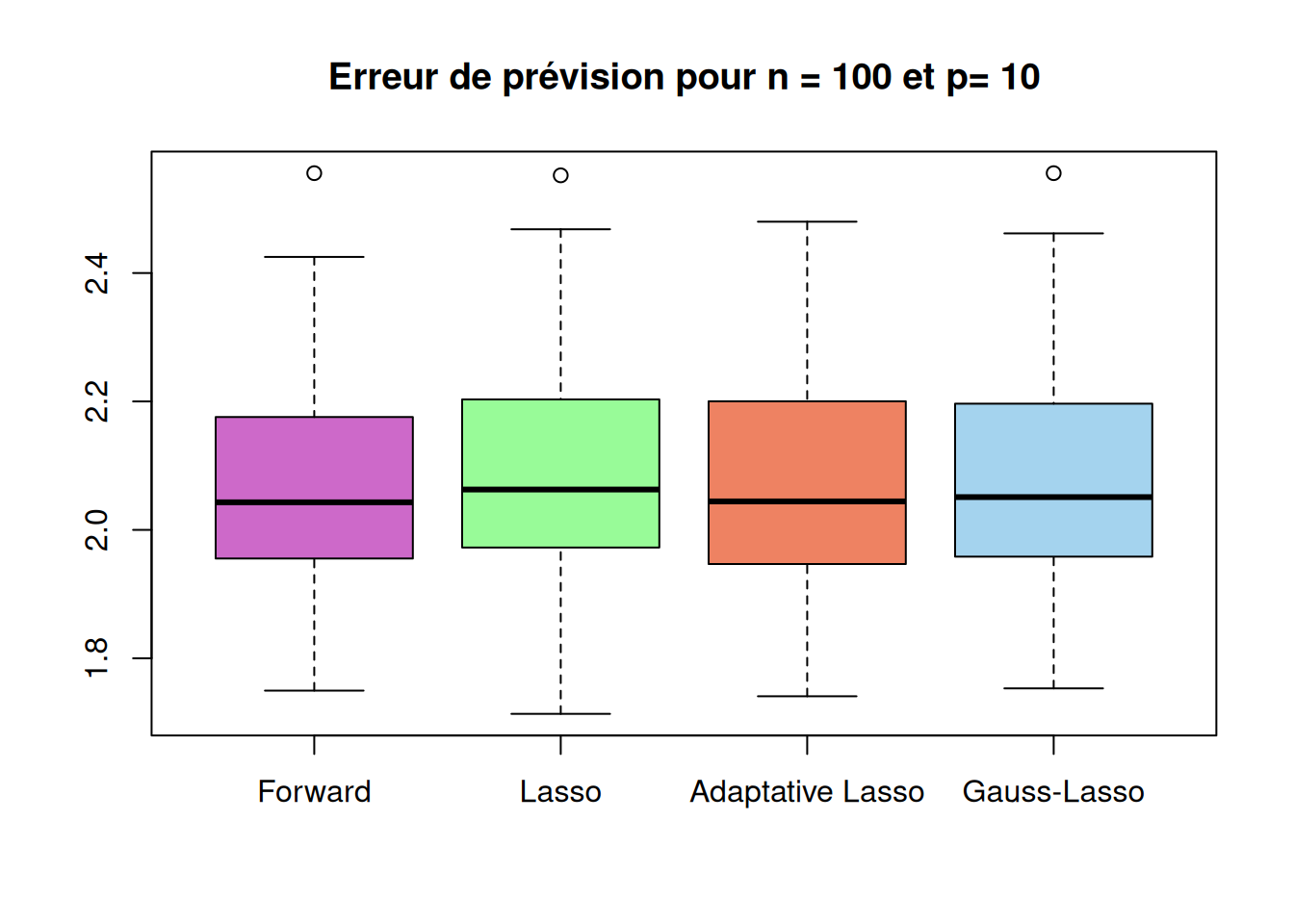
res_cas2 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas2$selec_method1,r_cas2$selec_method2,r_cas2$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas2$taille_method1),mean(r_cas2$taille_method2),mean(r_cas2$taille_method3),NA),
Prevision_error = c(mean(r_cas2$prev_method1),mean(r_cas2$prev_method2),mean(r_cas2$prev_method3),mean(r_cas2$prev_method4)),
Running_time = c(r_cas2$temps1,r_cas2$temps2,r_cas2$temps3,r_cas2$temps4)
)
t(res_cas2) [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection "0.01" "0.01" "0.10" NA
Mean_nb_selected_var " 8.11" "14.59" " 7.61" NA
Prevision_error "5.682778" "4.824673" "4.588443" "5.223387"
Running_time "0.13837" "0.06476" "0.09358" "0.09517" boxplot(sqrt(r_cas2$prev_method1),sqrt(r_cas2$prev_method2),sqrt(r_cas2$prev_method3),sqrt(r_cas2$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[2]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))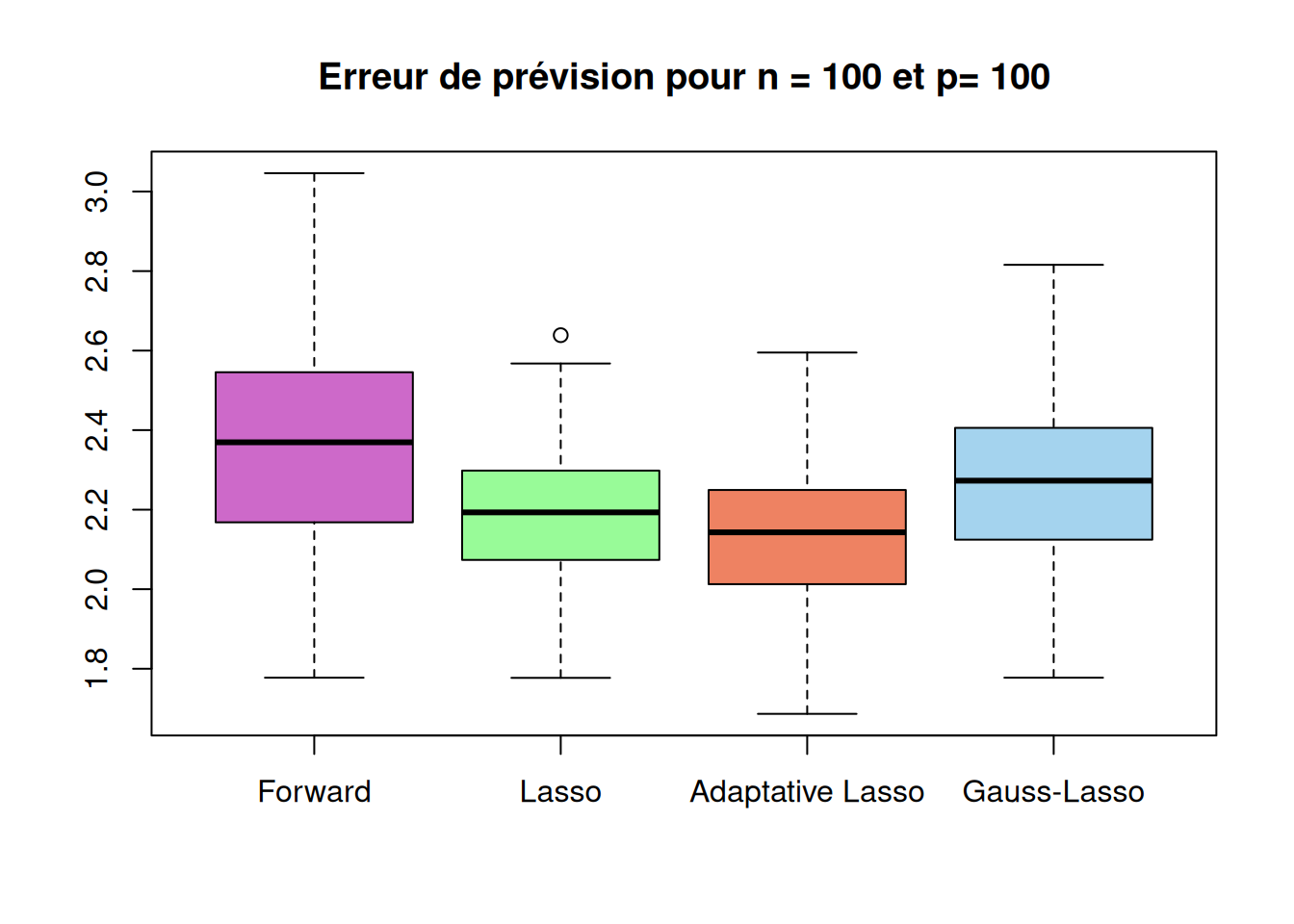
res_cas3 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas3$selec_method1,r_cas3$selec_method2,r_cas3$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas3$taille_method1),mean(r_cas3$taille_method2),mean(r_cas3$taille_method3),NA),
Prevision_error = c(mean(r_cas3$prev_method1),mean(r_cas3$prev_method2),mean(r_cas3$prev_method3),mean(r_cas3$prev_method4)),
Running_time = c(r_cas3$temps1,r_cas3$temps2,r_cas3$temps3,r_cas3$temps4)
)
t(res_cas3) [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection "0.00" "0.01" "0.16" NA
Mean_nb_selected_var "48.66" "17.34" " 7.73" NA
Prevision_error "11.428807" " 5.016189" " 4.523595" " 5.243494"
Running_time "2.67996" "0.06936" "0.10052" "0.10242" boxplot(sqrt(r_cas3$prev_method1),sqrt(r_cas3$prev_method2),sqrt(r_cas3$prev_method3),sqrt(r_cas3$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[3]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))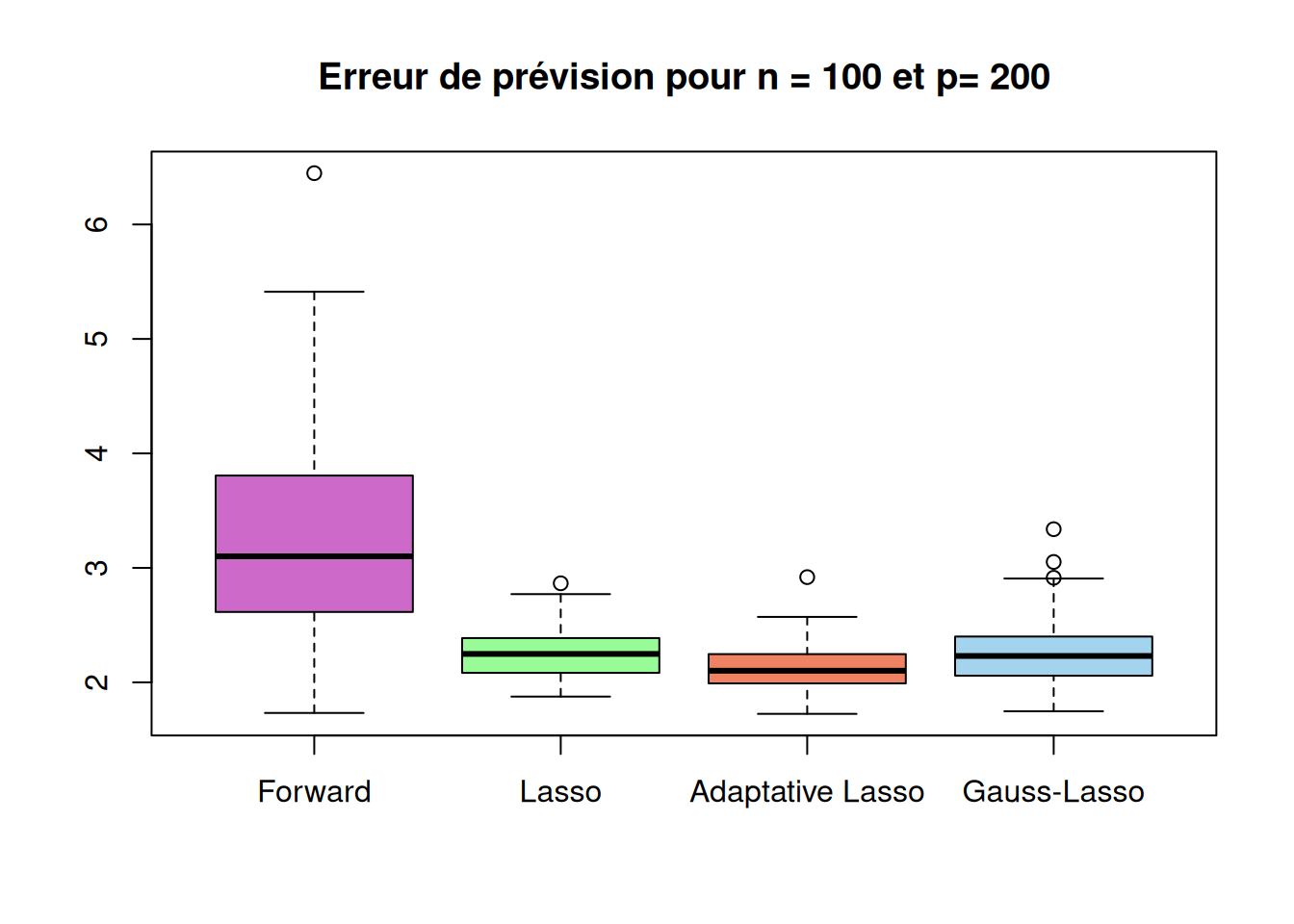
res_cas4 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas4$selec_method1,r_cas4$selec_method2,r_cas4$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas4$taille_method1),mean(r_cas4$taille_method2),mean(r_cas4$taille_method3),NA),
Prevision_error = c(mean(r_cas4$prev_method1),mean(r_cas4$prev_method2),mean(r_cas4$prev_method3),mean(r_cas4$prev_method4)),
Running_time = c(r_cas4$temps1,r_cas4$temps2,r_cas4$temps3,r_cas4$temps4)
)
t(res_cas4) [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection " 0" " 0" " 0" NA
Mean_nb_selected_var "99" "11" " 6" NA
Prevision_error "11.946047" " 5.699005" " 4.413508" " 5.439750"
Running_time "61.347" " 0.088" " 0.129" " 0.133" res_cas4bis = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas4bis$selec_method1,r_cas4bis$selec_method2,r_cas4bis$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas4bis$taille_method1),mean(r_cas4bis$taille_method2),mean(r_cas4bis$taille_method3),NA),
Prevision_error = c(mean(r_cas4bis$prev_method1),mean(r_cas4bis$prev_method2),mean(r_cas4bis$prev_method3),mean(r_cas4bis$prev_method4)),
Running_time = c(r_cas4bis$temps1,r_cas4bis$temps2,r_cas4bis$temps3,r_cas4bis$temps4)
)Warning in mean.default(r_cas4bis$taille_method1): l'argument n'est ni
numérique, ni logique : renvoi de NAWarning in mean.default(r_cas4bis$prev_method1): l'argument n'est ni numérique,
ni logique : renvoi de NA [,1] [,2] [,3] [,4]
Method "Forward" "Lasso" "Adaptative Lasso" "Gauss-Lasso"
Quality_of_selection NA "0.00" "0.03" NA
Mean_nb_selected_var NA "30.92" "11.07" NA
Prevision_error NA "5.260876" "4.776523" "5.836417"
Running_time NA "0.08522" "0.13196" "0.13632" boxplot(sqrt(r_cas4$prev_method1),sqrt(r_cas4$prev_method2),sqrt(r_cas4$prev_method3),sqrt(r_cas4$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[3]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))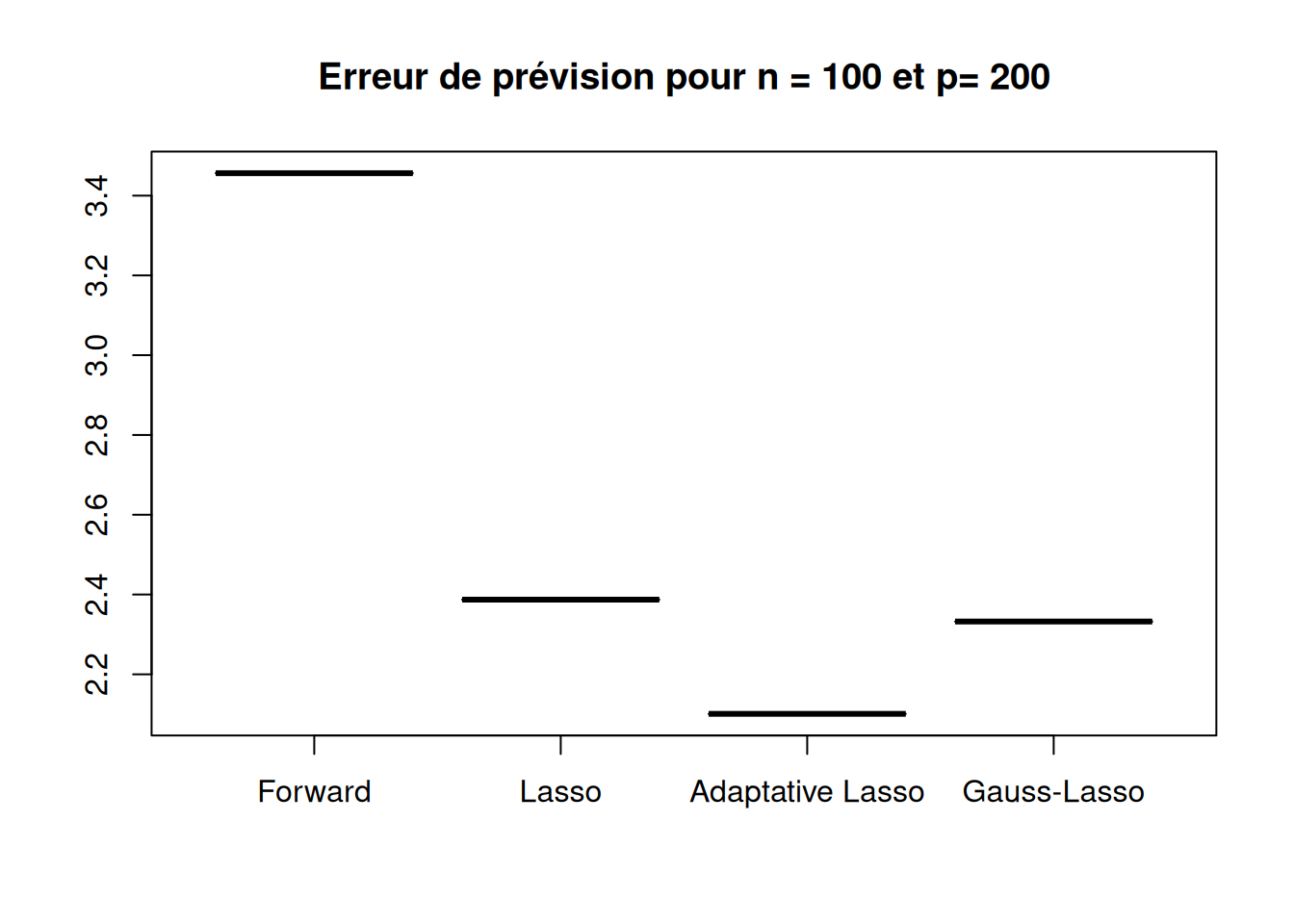
boxplot(sqrt(r_cas4$prev_method1),sqrt(r_cas4bis$prev_method2),sqrt(r_cas4bis$prev_method3),sqrt(r_cas4bis$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[4]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))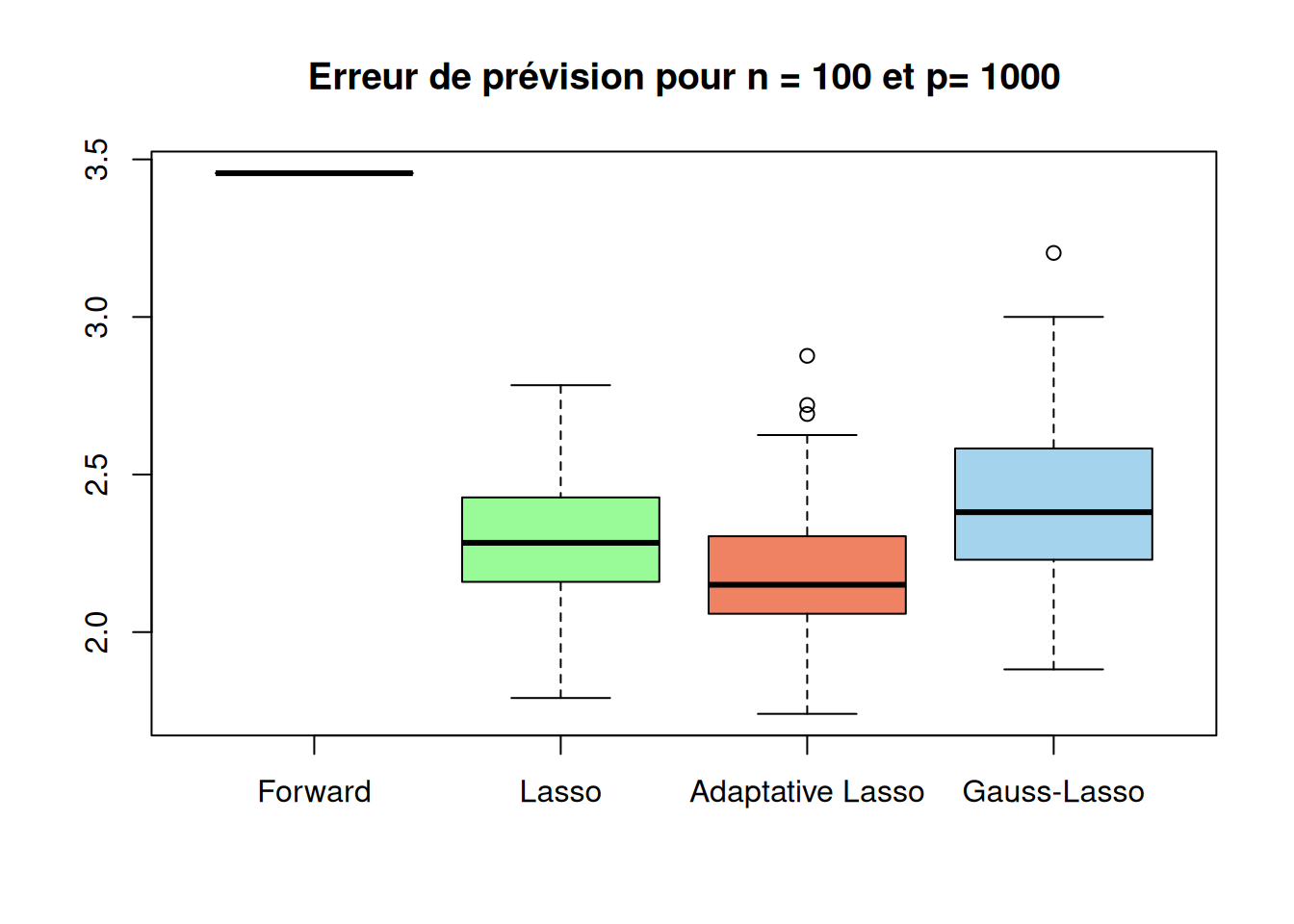
Conclure sur les mérites respectifs de chaque méthode dans le contexte de l’étude.
Quelles autres types de simulations pourrait-on envisager pour confirmer ou affiner ces conclusions ?
---
title: "Exercice 09"
author: "Clément Poupelin"
date: "2023-2024"
format:
html:
embed-resources: false
toc: true
code-fold: true
code-summary: "Show the code"
code-tools: true
toc-location: right
page-layout: article
code-overflow: wrap
toc: true
number-sections: false
editor: visual
categories: ["Régression Lasso", "Régression adaptative Lasso", "Régression Gauss-Lasso", "Sélection automatique"]
image: "/img/gants-de-boxe.png"
description: "Comparaison de différents modèles de regression"
---
```{r}
# On souhaite réaliser une petite étude par simulation pour évaluer
# les qualités respectives de 4 méthodes d’estimation d’un modèle de
# régression linéaire.
# On s’intéresse pour chacune d’elle à ses qualités de sélection de variables
# et à ses qualités prédictives. Le programme SimusReg.R permet de réaliser
# cette étude. Il contient deux fonctions, Simudata et la fonction
# principale fun, et un exemple d’utilisation en fin de programme.
## LE FAIRE EN RAPPORT SCIENTIFIQUE
# Question 1 ------------------------------------------------------------
#Simudata nous fait un modèle de regression linéaire multiple (lm avec p>4).
# notre bruit est gaussien
# y = 2*X1 + 2*X2 + 2*X3 + 0*X4 + eps (donc X4 n'intervient pas)
# Question 2 ------------------------------------------------------------
# avec fun on a :
# - forward hybride
# - alpha par defaut c'est ? LASSO
# - Lasso adaptative
# - Gauss-Lasso
# Question 3 ------------------------------------------------------------
# en sortie on a :
# - mean de ????
# - nb de var selectionnée (si selection)
# - erreur de prevision RMSEP
# - moyenne de temps de calcul
# The safe and reliable way to test two objects for being exactly equal.
# It returns TRUE in this case, FALSE in every other case.
# step$model renvoi les variables du modèle (noms et contenu)
# la première sortie nous dit si la méthode fait de la selection de variabel ou non
```
```{r setup, include=FALSE}
# chargement des packages et scripts nécessaires
library(latex2exp)
library(kableExtra)
library(corrplot)
library(scales)
library(ISLR)
library(leaps)
library(MASS)
library(psych) # pour pairs.panels
library(FactoMineR) # pour PCA
library(GGally) # pour ggcorr
library(car) # pour VIF
library(dplyr)
library(future)
set.seed(123)
```
On souhaite réaliser une petite étude par simulation pour évaluer les qualités respectives de 4 méthodes d’estimation d’un modèle de régression linéaire. On s’intéresse pour chacune d’elle à ses qualités de sélection de variables et à ses qualités prédictives. Le programme SimusReg.R permet de réaliser cette étude. Il contient deux fonctions, Simudata et la fonction principale fun, et un exemple d’utilisation en fin de programme.
```{r}
n = 100
p = 500
X = matrix(rnorm(n*p), n, p)
```
```{r function}
library(lars)
library(leaps)
library(glmnet)
DataSimulation = function(n,p){
if(p < 4){stop("p>3 require")}
# We create our matrix of explanatory variables
X = matrix(rnorm(n*p), n, p)
# We define our coefficients of regression
coeff = matrix(0, p)
coeff[1:3] = 2
# We build our explanatory variables
y = X%*%coeff + rnorm(n, sd = 2)
return(list(X = X, y = y, coeff = coeff))
}
fun = function(n, p, M = 100){ # By default, we make M = 100 simulation
## Initialization
#################
selec_method1 = NULL; selec_method2 = NULL; selec_method3 = NULL;
taille_method1 = NULL; taille_method2 = NULL; taille_method3 = NULL;
prev_method1 = NULL; prev_method2 = NULL; prev_method3 = NULL; prev_method4 = NULL;
temps1 = NULL; temps2 = NULL; temps3 = NULL; temps4 = NULL;
for(i in 1:M){
cat(paste(i, ":")) # counter to see progress
# We define our train set
datatrain = DataSimulation(n, p)
Xtrain = datatrain$X
y = datatrain$y
coeff = datatrain$coeff
# We define our test set
datatest = DataSimulation(n, p)
Xtest = datatest$X
ytest = datatest$y
## Regression
#################
# Method 1 : Forward-Hybrid with BIC
tic = proc.time()
tab = data.frame(y = y, X = Xtrain)
fit0 = lm(y~1, tab)
fit = lm(y~., tab)
tmp = step(fit0, scope = formula(fit),
k = log(n), # BIC criteria
direction = "both", # Hybrid
trace = 0)
noms = sort(names(tmp$model))
selec_method1[i] = identical(
noms[-length(noms)], sort(paste("X.", which(coeff != 0), sep = ""))
)
taille_method1[i] = length(noms) - 1
prev_method1[i] = mean((predict(tmp,data.frame(X = Xtest)) - ytest)^2)
tac = proc.time() - tic
temps1[i] = tac[3]
# Method 2 : Lasso
tic = proc.time()
cvglm = cv.glmnet(Xtrain, y) # By default we have Lasso
lambda = cvglm$lambda.min
coef2 = coef(cvglm, s = lambda)[-1]
index = which(coef2 != 0)
selec_method2[i] = identical(sort(index), which(coeff != 0))
taille_method2[i] = length(index)
prev_method2[i] = mean((predict(cvglm, Xtest, s = lambda) - ytest)^2)
tac = proc.time() - tic
temps2[i] = tac[3]
# Methods 3 and 4 : Adaptive Lasso and Gauss-Lasso
if(length(index) == 0){
selec_method3[i] = selec_method2[i]
taille_method3[i] = taille_method2[i]
prev_method3[i] = prev_method2[i]
prev_method4[i] = prev_method2[i]}
else{
# Adaptive Lasso part
cvglm = cv.glmnet(Xtrain, y,
penalty.factor = 1/abs(coef2))
lambda = cvglm$lambda.min
coef3 = coef(cvglm, s = lambda)[-1]
index = which(coef3 != 0)
selec_method3[i] = identical(sort(index), which(coeff != 0))
taille_method3[i] = length(index)
prev_method3[i] = mean((predict(cvglm, Xtest, s = lambda) - ytest)^2)
tac = proc.time() - tic
temps3[i] = tac[3]
# Gauss-Lasso part
if(length(index) == 0){
prev_method4[i] = mean((mean(y) - ytest)^2)}
else{
tab = data.frame(y = y, X = Xtrain)
reg = lm(y~.,
data = tab[, c(1, index + 1)])
prev_method4[i] = mean((predict(reg, data.frame(X = Xtest)) - ytest)^2)
tac = proc.time() - tic
temps4[i] = tac[3]
}
}
}
## Results
#################
res = list(mean(selec_method1), mean(selec_method2), mean(selec_method3), taille_method1, taille_method2, taille_method3, prev_method1, prev_method2, prev_method3, prev_method4, mean(temps1), mean(temps2), mean(temps3), mean(temps4))
names(res) = c("selec_method1", "selec_method2", "selec_method3", "taille_method1", "taille_method2", "taille_method3", "prev_method1", "prev_method2", "prev_method3", "prev_method4", "temps1", "temps2", "temps3", "temps4")
return(res)
}
fun2 = function(n, p, M = 100){ # By default, we make M = 100 simulation
## Initialization
#################
selec_method1 = NULL; selec_method2 = NULL; selec_method3 = NULL;
taille_method1 = NULL; taille_method2 = NULL; taille_method3 = NULL;
prev_method1 = NULL; prev_method2 = NULL; prev_method3 = NULL; prev_method4 = NULL;
temps1 = NULL; temps2 = NULL; temps3 = NULL; temps4 = NULL;
for(i in 1:M){
cat(paste(i, ":")) # counter to see progress
# We define our train set
datatrain = DataSimulation(n, p)
Xtrain = datatrain$X
y = datatrain$y
coeff = datatrain$coeff
# We define our test set
datatest = DataSimulation(n, p)
Xtest = datatest$X
ytest = datatest$y
## Regression
#################
# Method 2 : Lasso
tic = proc.time()
cvglm = cv.glmnet(Xtrain, y) # By default we have Lasso
lambda = cvglm$lambda.min
coef2 = coef(cvglm, s = lambda)[-1]
index = which(coef2 != 0)
selec_method2[i] = identical(sort(index), which(coeff != 0))
taille_method2[i] = length(index)
prev_method2[i] = mean((predict(cvglm, Xtest, s = lambda) - ytest)^2)
tac = proc.time() - tic
temps2[i] = tac[3]
# Methods 3 and 4 : Adaptive Lasso and Gauss-Lasso
if(length(index) == 0){
selec_method3[i] = selec_method2[i]
taille_method3[i] = taille_method2[i]
prev_method3[i] = prev_method2[i]
prev_method4[i] = prev_method2[i]}
else{
# Adaptive Lasso part
cvglm = cv.glmnet(Xtrain, y,
penalty.factor = 1/abs(coef2))
lambda = cvglm$lambda.min
coef3 = coef(cvglm, s = lambda)[-1]
index = which(coef3 != 0)
selec_method3[i] = identical(sort(index), which(coeff != 0))
taille_method3[i] = length(index)
prev_method3[i] = mean((predict(cvglm, Xtest, s = lambda) - ytest)^2)
tac = proc.time() - tic
temps3[i] = tac[3]
# Gauss-Lasso part
if(length(index) == 0){
prev_method4[i] = mean((mean(y) - ytest)^2)}
else{
tab = data.frame(y = y, X = Xtrain)
reg = lm(y~.,
data = tab[, c(1, index + 1)])
prev_method4[i] = mean((predict(reg, data.frame(X = Xtest)) - ytest)^2)
tac = proc.time() - tic
temps4[i] = tac[3]
}
}
}
## Results
#################
res = list(mean(selec_method1), mean(selec_method2), mean(selec_method3), taille_method1, taille_method2, taille_method3, prev_method1, prev_method2, prev_method3, prev_method4, mean(temps1), mean(temps2), mean(temps3), mean(temps4))
names(res) = c("selec_method1", "selec_method2", "selec_method3", "taille_method1", "taille_method2", "taille_method3", "prev_method1", "prev_method2", "prev_method3", "prev_method4", "temps1", "temps2", "temps3", "temps4")
return(res)
}
```
```{r}
###### Exemple
a=fun(50,5,100)
```
```{r}
a$selec_method1
a$selec_method2
a$selec_method3
a$taille_method1
a$taille_method2
a$taille_method3
boxplot(sqrt(a$prev_method1),sqrt(a$prev_method2),sqrt(a$prev_method3),sqrt(a$prev_method4),names=c("Method1","Method2","Method3","Method4"),main="Title")
mean(a$prev_method1)
mean(a$prev_method2)
mean(a$prev_method3)
mean(a$prev_method4)
a$temps1
a$temps2
a$temps3
a$temps4
```
### Question 1
Quel modèle génère la fonction Simudata ? Combien de variables explicatives sont générées ? Parmi elles, lesquelles sont pertinentes pour la modélisation ? Ecrire l’équation du modèle.
### Question 2
Identifier les 4 méthodes d’estimation mises en oeuvre dans la fonction fun.
### Question 3
Détailler les différentes sorties proposées par la fonction fun.
### Question 4
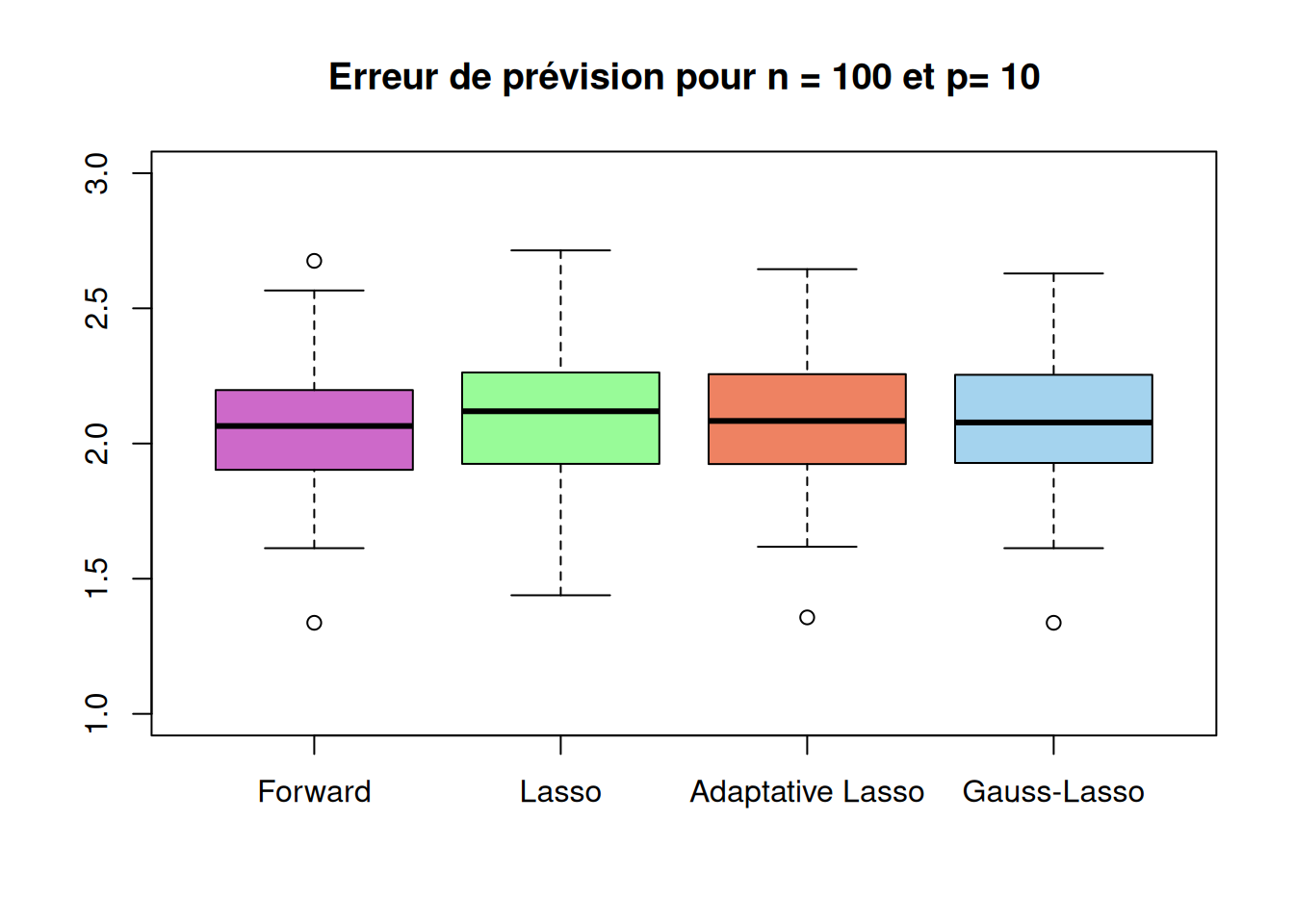
Remplacer la valeur des options names et title du boxplot réalisé dans l’exemple par les bonnes informations.
```{r}
boxplot(sqrt(a$prev_method1),sqrt(a$prev_method2),sqrt(a$prev_method3),sqrt(a$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", 100,"et p=", 10),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"),
ylim = c(1,3))
```
### Question 5
Réaliser une étude comparative des méthodes lorsque $n = 50$ et $p = n/10$, $p = n$, $p = 2n$, $p = 10n$. Pour chaque situation, on considèrera $100$ simulations afin de calculer les différents critères. On synthétisera les résultats en terme de qualité de sélection, nombre de variables sélectionnées, erreurs de prévision et temps de calcul.
```{r, warning=FALSE}
#parallelisation
future::plan(multisession, workers = 2)
n = 50
p_list = c(n/10, n, 2*n, 10*n)
r_cas1 = fun(n, p_list[1])
r_cas2 = fun(n, p_list[2])
r_cas3 = fun(n, p_list[3])
r_cas4 = fun(n, p_list[4],1)
r_cas4bis = fun2(n, p_list[4])
# file_path <- file.path("../Data/r_cas1.rds")
# saveRDS(r_cas1, file = file_path)
# quit parallelisation
future::plan("sequential")
```
```{r}
# file_path <- file.path("../Data/r_cas1.rds")
# r_cas1 <- readRDS(file_path)
```
```{r}
res_cas1 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas1$selec_method1,r_cas1$selec_method2,r_cas1$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas1$taille_method1),mean(r_cas1$taille_method2),mean(r_cas1$taille_method3),NA),
Prevision_error = c(mean(r_cas1$prev_method1),mean(r_cas1$prev_method2),mean(r_cas1$prev_method3),mean(r_cas1$prev_method4)),
Running_time = c(r_cas1$temps1,r_cas1$temps2,r_cas1$temps3,r_cas1$temps4)
)
t(res_cas1)
boxplot(sqrt(r_cas1$prev_method1),sqrt(r_cas1$prev_method2),sqrt(r_cas1$prev_method3),sqrt(r_cas1$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[1]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
```{r}
res_cas2 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas2$selec_method1,r_cas2$selec_method2,r_cas2$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas2$taille_method1),mean(r_cas2$taille_method2),mean(r_cas2$taille_method3),NA),
Prevision_error = c(mean(r_cas2$prev_method1),mean(r_cas2$prev_method2),mean(r_cas2$prev_method3),mean(r_cas2$prev_method4)),
Running_time = c(r_cas2$temps1,r_cas2$temps2,r_cas2$temps3,r_cas2$temps4)
)
t(res_cas2)
boxplot(sqrt(r_cas2$prev_method1),sqrt(r_cas2$prev_method2),sqrt(r_cas2$prev_method3),sqrt(r_cas2$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[2]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
```{r}
res_cas3 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas3$selec_method1,r_cas3$selec_method2,r_cas3$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas3$taille_method1),mean(r_cas3$taille_method2),mean(r_cas3$taille_method3),NA),
Prevision_error = c(mean(r_cas3$prev_method1),mean(r_cas3$prev_method2),mean(r_cas3$prev_method3),mean(r_cas3$prev_method4)),
Running_time = c(r_cas3$temps1,r_cas3$temps2,r_cas3$temps3,r_cas3$temps4)
)
t(res_cas3)
boxplot(sqrt(r_cas3$prev_method1),sqrt(r_cas3$prev_method2),sqrt(r_cas3$prev_method3),sqrt(r_cas3$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[3]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
```{r}
res_cas4 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas4$selec_method1,r_cas4$selec_method2,r_cas4$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas4$taille_method1),mean(r_cas4$taille_method2),mean(r_cas4$taille_method3),NA),
Prevision_error = c(mean(r_cas4$prev_method1),mean(r_cas4$prev_method2),mean(r_cas4$prev_method3),mean(r_cas4$prev_method4)),
Running_time = c(r_cas4$temps1,r_cas4$temps2,r_cas4$temps3,r_cas4$temps4)
)
t(res_cas4)
boxplot(sqrt(r_cas4$prev_method1),sqrt(r_cas4$prev_method2),sqrt(r_cas4$prev_method3),sqrt(r_cas4$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[3]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
```{r}
res_cas4bis = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas4bis$selec_method1,r_cas4bis$selec_method2,r_cas4bis$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas4bis$taille_method1),mean(r_cas4bis$taille_method2),mean(r_cas4bis$taille_method3),NA),
Prevision_error = c(mean(r_cas4bis$prev_method1),mean(r_cas4bis$prev_method2),mean(r_cas4bis$prev_method3),mean(r_cas4bis$prev_method4)),
Running_time = c(r_cas4bis$temps1,r_cas4bis$temps2,r_cas4bis$temps3,r_cas4bis$temps4)
)
t(res_cas4bis)
boxplot(sqrt(r_cas4$prev_method1),sqrt(r_cas4bis$prev_method2),sqrt(r_cas4bis$prev_method3),sqrt(r_cas4bis$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[4]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
### Question 6
Réaliser la même étude pour $n = 100$ et $p = n/10$, $p = n$, $p = 2n$, toujours basée sur $100$ simulations dans chaque cas. Considérer de plus le cas $p = 10n$ en ne faisant qu’une seule simulation afin d’en évaluer le temps de calcul. Une fois ce temps analysé, lancer $100$ simulations pour $p = 10n$ mais en omettant la méthode la plus couteuse en temps de calcul.
```{r, warning=FALSE}
#parallelisation
future::plan(multisession, workers = 2)
n = 100
p_list = c(n/10, n, 2*n, 10*n)
r_cas1 = fun(n, p_list[1])
r_cas2 = fun(n, p_list[2])
r_cas3 = fun(n, p_list[3])
r_cas4 = fun(n, p_list[4],1)
r_cas4bis = fun2(n, p_list[4])
# quit parallelisation
future::plan("sequential")
```
```{r}
res_cas1 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas1$selec_method1,r_cas1$selec_method2,r_cas1$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas1$taille_method1),mean(r_cas1$taille_method2),mean(r_cas1$taille_method3),NA),
Prevision_error = c(mean(r_cas1$prev_method1),mean(r_cas1$prev_method2),mean(r_cas1$prev_method3),mean(r_cas1$prev_method4)),
Running_time = c(r_cas1$temps1,r_cas1$temps2,r_cas1$temps3,r_cas1$temps4)
)
t(res_cas1)
boxplot(sqrt(r_cas1$prev_method1),sqrt(r_cas1$prev_method2),sqrt(r_cas1$prev_method3),sqrt(r_cas1$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[1]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
```{r}
res_cas2 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas2$selec_method1,r_cas2$selec_method2,r_cas2$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas2$taille_method1),mean(r_cas2$taille_method2),mean(r_cas2$taille_method3),NA),
Prevision_error = c(mean(r_cas2$prev_method1),mean(r_cas2$prev_method2),mean(r_cas2$prev_method3),mean(r_cas2$prev_method4)),
Running_time = c(r_cas2$temps1,r_cas2$temps2,r_cas2$temps3,r_cas2$temps4)
)
t(res_cas2)
boxplot(sqrt(r_cas2$prev_method1),sqrt(r_cas2$prev_method2),sqrt(r_cas2$prev_method3),sqrt(r_cas2$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[2]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
```{r}
res_cas3 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas3$selec_method1,r_cas3$selec_method2,r_cas3$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas3$taille_method1),mean(r_cas3$taille_method2),mean(r_cas3$taille_method3),NA),
Prevision_error = c(mean(r_cas3$prev_method1),mean(r_cas3$prev_method2),mean(r_cas3$prev_method3),mean(r_cas3$prev_method4)),
Running_time = c(r_cas3$temps1,r_cas3$temps2,r_cas3$temps3,r_cas3$temps4)
)
t(res_cas3)
boxplot(sqrt(r_cas3$prev_method1),sqrt(r_cas3$prev_method2),sqrt(r_cas3$prev_method3),sqrt(r_cas3$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[3]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
```{r}
res_cas4 = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas4$selec_method1,r_cas4$selec_method2,r_cas4$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas4$taille_method1),mean(r_cas4$taille_method2),mean(r_cas4$taille_method3),NA),
Prevision_error = c(mean(r_cas4$prev_method1),mean(r_cas4$prev_method2),mean(r_cas4$prev_method3),mean(r_cas4$prev_method4)),
Running_time = c(r_cas4$temps1,r_cas4$temps2,r_cas4$temps3,r_cas4$temps4)
)
t(res_cas4)
res_cas4bis = data.frame(
Method = c("Forward", "Lasso", "Adaptative Lasso", "Gauss-Lasso"),
Quality_of_selection = c(r_cas4bis$selec_method1,r_cas4bis$selec_method2,r_cas4bis$selec_method3,NA),
Mean_nb_selected_var = c(mean(r_cas4bis$taille_method1),mean(r_cas4bis$taille_method2),mean(r_cas4bis$taille_method3),NA),
Prevision_error = c(mean(r_cas4bis$prev_method1),mean(r_cas4bis$prev_method2),mean(r_cas4bis$prev_method3),mean(r_cas4bis$prev_method4)),
Running_time = c(r_cas4bis$temps1,r_cas4bis$temps2,r_cas4bis$temps3,r_cas4bis$temps4)
)
t(res_cas4bis)
boxplot(sqrt(r_cas4$prev_method1),sqrt(r_cas4$prev_method2),sqrt(r_cas4$prev_method3),sqrt(r_cas4$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[3]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
boxplot(sqrt(r_cas4$prev_method1),sqrt(r_cas4bis$prev_method2),sqrt(r_cas4bis$prev_method3),sqrt(r_cas4bis$prev_method4),
names=c("Forward","Lasso","Adaptative Lasso","Gauss-Lasso"),
main=paste("Erreur de prévision pour n =", n,"et p=", p_list[4]),
col = c("orchid3", "palegreen", "salmon2", "lightskyblue2"))
```
### Question 7
Conclure sur les mérites respectifs de chaque méthode dans le contexte de l’étude.
### Question 8
Quelles autres types de simulations pourrait-on envisager pour confirmer ou affiner ces conclusions ?