Dans cette partie et avant de passer à l’exercice 7, nous allons faire la section 3.1 sur la regression Ridge et Lasso avec glmnet sous R du tutoriel de Laurent Rouvière

Rappels sur Ridge et Lasso

On se base encore ici sur notre modèle classique de régression linéaire :

\[y = X\beta + \mathcal{E} \quad \text{ou} \quad y = \beta_0 + \beta_1X^1 + ... + \beta_pX^p + \mathcal{E}\]

$y \in \mathbb{R}^{n}$ la variable réponse ou variable à expliquer
$X \in \mathbb{R}^{n\times (p+1)}$ la matrice déterministe contenant nos $p$ variables explicatives
$\beta \in \mathbb{R}^{p+1}$ le vecteur qui contient les coefficients de régression $\beta_0, ..., \beta_p$ que nous cherchons à estimer
$\mathcal{E} \in \mathbb{R}^{n}$ le vecteur d’erreur qui n’est pas corrélé à nos variables explicatives. C’est la part d’aléa que nous n’arrivons pas à déterminer

Pour l’estimation des coefficients de regression de ce type de modèle, nous utilisons souvent la méthodes des moindres carrées ordinaire (MCO) qui nous donne

\[\hat{\beta} = \underset{\beta}{argmin}||y-X\beta||^2\] Malheureusement, lorsque $p$ est grand ou que les variables sont linéairement dépendantes, les estimateurs des moindres carrées peuvent être mis en défaut. Les méthodes pénalisées ou sous contraintes consistent alors à restreindre l’espace sur lequel on minimise ce critère.

L’idée principale de ces méthodes est de contraindre la valeur des estimateurs MCO pour réduire la variance, quitte à augmenter un peu le biais (d’où la terminologie de “régression biaisée”). Nous obtenons donc, pour un certain $t>0$, des estimations de la forme suivante : \[ \hat{\beta}^{pen} = \underset{\beta}{argmin}||y-X\beta||^2 \quad \text{sous la contrainte} \quad ||\beta||? \leq t\]

Ridge
Lasso

La régression Ridge contraint la norme $\ell^2$ des coefficients $\beta$ à ne pas exploser, i.e $||\beta||_2 = \sum_{j=0}^{p} \beta_j^2 \leq t$. Cela conduit à la solution d’optimisation suivante :

\[ \hat{\beta}_{Ridge} = \underset{\beta}{\operatorname{argmin}} \ ||y - X\beta||^2 \quad \text{sous la contrainte} \quad \sum_{j=0}^{p} \beta_j^2 \leq t \]

où $\hat{\beta}_{Ridge}$ est unique, contrairement à Lasso qui peut produire plusieurs solutions.

Contrairement à Lasso, Ridge ne met pas exactement à zéro certains coefficients, mais réduit leur valeur. Il n’y a donc pas de sélection de variable effectué.
Cette méthode est tout de même robuste en grande dimension et particulièrement utile lorsque les variables sont fortement corrélées. Il empêche les coefficients de devenir trop grands, ce qui réduit la variance du modèle.

La régression Lasso (pour Least Absolute Shrinkage and Selection Operator) contraint la norme $\ell^1$ de $\beta$ à ne pas exploser, i.e $||\beta||_1 = \sum_{j=0}^{p} |\beta_j| \leq t$. Nous obtenons donc

\[\hat{\beta}_{Lasso} = \underset{\beta}{argmin}||y-X\beta||^2 \quad \text{sous la contrainte} \quad \sum_{j=0}^{p} |\beta_j| \leq t \]

Où $\hat{\beta}_{Lasso}$ n’est pas nécessairement unique mais la prévision $\hat{y} = X\hat{\beta}_{Lasso}$ est unique.

Cette méthode est principalement caractérisée par le fait qu’elle est robuste à la grande dimension en sélectionnant les variables les plus pertinentes. En effet, elle nous permet de réduire les coefficients MCO des variables sélectionnées en rapprochant leur valeur de 0, ce qui est appelé la propriété de “seuillage doux” du Lasso.

Ici, il sera donc présenté les étapes principales qui permettent de faire ce type de régression avec R. Le package le plus souvent utilisé est glmnet.

Setup

Packages
Fonctions

Show the code

# Inférence
library(glmnet) ## regression pénalisée

# Plots
## ggplot
library(ggplot2)
library(gridExtra)

Show the code

my_boxplot <- function(data) {
  data_long <- reshape2::melt(data)
  
  ggplot(data_long, aes(x = variable, y = value, fill = variable)) +
    geom_boxplot() +
    scale_fill_viridis_d() +  # Palette de couleurs harmonieuse
    labs(title = "Distribution des Variables (Boxplot)", x = "Variables", y = "Valeurs") +
    theme_minimal() +  # Thème épuré
    theme(axis.text.x = element_text(angle = 45, hjust = 1))  # Rotation des étiquettes
}

Show the code

my_pairs.panels <- function(data) {
  psych::pairs.panels(
    data,
    method = "pearson",
    # Méthode de corrélation
    hist.col = RColorBrewer::brewer.pal(9, "Set3"),
    # Couleurs des histogrammes
    density = TRUE,
    # Ajout des courbes de densité
    ellipses = TRUE,
    # Ajout d'ellipses
    smooth = TRUE,
    # Ajout de régressions lissées
    lm = TRUE,
    # Ajout des droites de régression
    col = "#69b3a2",
    # Couleur des points
    alpha = 0.5              # Transparence
  )
}

Show the code

cv_ridge_vs_lasso <- function(data, fmla) {
  set.seed(140400)
  
  data.X <- model.matrix(fmla, data = data)[, -1]
  data.Y <- data$maxO3
  
  blocs <- caret::createFolds(1:nrow(data), k = 10)
  
  prev <- matrix(0, ncol = 3, nrow = nrow(data)) %>%  as.data.frame()
  names(prev) <- c("Linéaire (MCO)", "Ridge", "Lasso")
  for (k in 1:10) {
    app <- data[-blocs[[k]], ]
    test <- data[blocs[[k]], ]
    
    app.X <- data.X[-blocs[[k]], ]
    app.Y <- data.Y[-blocs[[k]]]
    
    test.X <- data.X[blocs[[k]], ]
    test.Y <- data.Y[blocs[[k]]]
    
    ridge <- cv.glmnet(app.X, app.Y, alpha = 0)
    lasso <- cv.glmnet(app.X, app.Y, alpha = 1)
    lin <- lm(fmla, data = app)
    
    prev[blocs[[k]], ] <- tibble::tibble(
      lin = predict(lin, newdata = test),
      ridge = as.vector(predict(ridge, newx =
                                  test.X)),
      lasso = as.vector(predict(lasso, newx =
                                  test.X))
    )
  }
  
  err <- prev %>%  mutate(obs = data$maxO3) %>%  summarise_at(1:3, ~ mean((obs -
                                                                             .)^2))
  return(err)
}

Données

On considère le jeu de données ozone.txt où on cherche à expliquer la concentration maximale en ozone relevée sur une journée (variable maxO3) par d’autres variables essentiellement météorologiques.

La base de données d’origine ozone.txt répertorie ainsi 112 données météorologiques mesurées durant l’été 2001 à Rennes. Celles-ci sont caractérisées par les 13 variables suivantes :

maxO3	concentration maximale d'ozone (en DU)
T9	température à 9H (en °C)
T12	température à 12H (en °C)
T15	température à 15H (en °C)
Ne9	nébulosité à 9H (en octa)
Ne12	nébulosité à 12H (en octa)
Ne15	nébulosité à 15H (en octa)
Vx9	vitesse du vent à 9H
Vx12	vitesse du vent à 12H
Vx15	vitesse du vent à 15H
maxO3v	concentration maximale d'ozone de la veille (en DU)
vent	direction principale du vent (Nord / Ouest / Sud / Est)
pluie	présence ou non de pluie (Sec / Pluie)

On identifie le regroupement de toutes les données météorologiques récoltées en une journée par la date à laquelle les relevés ont été effectués.

Show the code

ozone <-read.table("https://r-stat-sc-donnees.github.io/ozone.txt", header=TRUE)
ozone %>% DT::datatable()

Note

Bien évidémment on a vérifié qu’il n’y a pas de valeurs manquantes dans cette base de données avec la fonction anyNA qui renvoie FALSE

Analyse descriptive

On peut regarder un peu la distribution de nos différents variables quantitatives via des boxplots.

Show the code

my_boxplot(ozone)

Résultats

On remarque bien que les variabeles qui sont de même nature mais à des points de temps différents sont d’avantages similaires.

Pour confirmer cela, on peut faire des boxplot pour uniquement une varibale et ses différents points de temps.

Show the code

subset(ozone, select = c("T9", "T12", "T15"))  %>% my_boxplot()

Show the code

subset(ozone, select = c("Ne9", "Ne12", "Ne15"))  %>% my_boxplot()

Show the code

subset(ozone, select = c("Vx9", "Vx12", "Vx15"))  %>% my_boxplot()

On regarde ici la corrélation calculée entre chacune de nos variables.

Show the code

my_pairs.panels(ozone)

Résultats

On voit la présence de plusieurs fortes corrélations qui peut déjà nous alerter si l’on veut faire des modèles de regressions linéaires car on risque d’avoir un problème de colinéarité entre les varibales explicatives.

Cependant ces corrélation fortes sont surtout présentes pour les variables qui sont à différents points de temps ce qui est logique.

Avec une Analyse en Composantes Principales (PCA) on peut regarder un peu le comportement de nos données.

En effet, Cette méthode respose sur la transformation des variables d’origine en nouvelles variables non corrélées, appelées composantes principales, qui capturent successivement la plus grande variance possible des données.

Show the code

res_pca <- FactoMineR::PCA(
  ozone,
  quali.sup = c(which(colnames(ozone) %in% c("vent", "pluie"))),
  quanti.sup = c(which(colnames(ozone) %in% c("max03", "max03v"))),
  graph = FALSE
)

Ici, on spécifi nos varibales qualitatives et on décide de mettre la variable max03 et max03v en variable supplémentaire, ce qui veut d’ire qu’elles ne seront pas considérés pour la formation de nos composantes principales (variable que l’on cherchera à estimer plus tard).

Tout d’abord, on peut commencer par regarder le pourcentage de variance expliqué par nos différentes composantes principales.

Show the code

factoextra::fviz_eig(
  res_pca,
  ncp = 10,
  addlabels = TRUE,
  barfill = "coral",
  barcolor = "coral",
  ylim = c(0, 60),
  main = "Percentage of variance of the 10 first components"
)

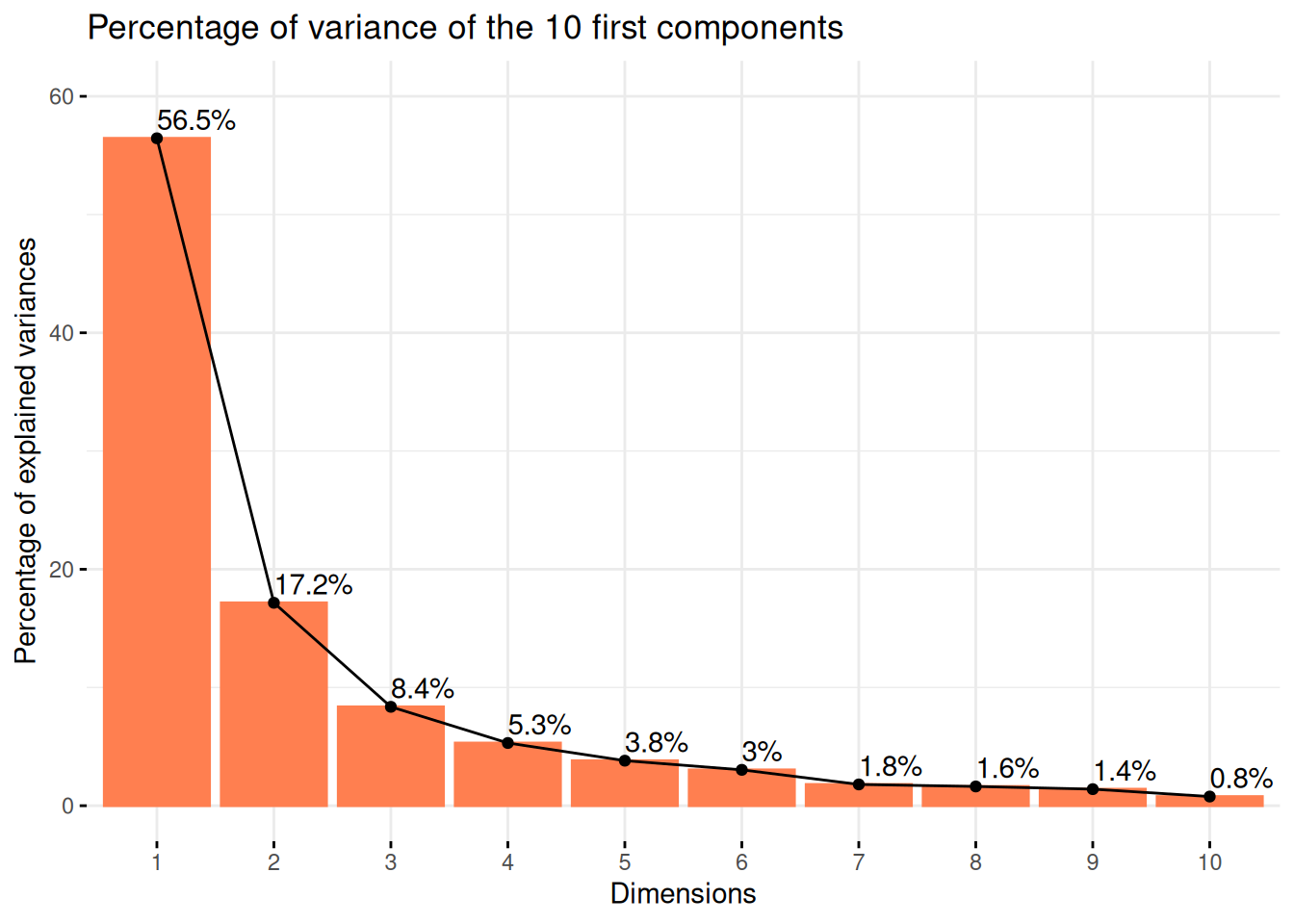
Résultats

On voit ainsi que la majorité de la variance est expliquée par nos deux premières composantes principales.

Le plan des individus est une projection des observations sur les axes principaux de la PCA. Cette visualisation permet d’identifier des regroupements, tendances et anomalies au sein des données.

Ainsi, des individus proches sur le graphique ont des caractéristiques similaires par rapport aux variables utilisées.

Puis, le placement d’un individu en fonction des axes peut permettre de savoir comment le jouer se caractérise par rapport aux variables qui contribuent le plus à ces axes.

Pluie
vent

Show the code

factoextra::fviz_pca_ind(
  res_pca,
  label = "none",
  pointsize = 2,
  habillage = as.factor(ozone$pluie),
  addEllipses = TRUE,
  ellipse.level = 0.95
)

Show the code

factoextra::fviz_pca_ind(
  res_pca,
  label = "none",
  pointsize = 2,
  habillage = as.factor(ozone$vent),
  addEllipses = TRUE,
  ellipse.level = 0.95
)

Résultats

Ici on voit une repartition plutot uniforme sur le plan qui ne semble pas permettre de distinguer une séparation forte correspodant à nos variables qualitatives.

Le cercle des variables est une représentation graphique qui permet d’analyser les relations entre les variables initiales et les composantes principales qui forment nos axes. Il est basé sur les corrélations entre les variables et les axes principaux.

Ainsi, plus une variable est proche du bord du cercle, plus elle est bien représentée sur le plan factoriel et contribue fortement à la formation des axes. Ici, on utilise le cos2 pour le gradient de couleur qui va aider à l’indentifictation de ces différentes qualitées de représentation.

De plus, selon l’angle entre deux varibles, on peut faire des suppositions sur leur corrélation :

Si deux variables ont des vecteurs proches (petit angle), elles sont fortement corrélées positivement
Si deux variables ont des vecteurs opposés (angle proche de 180°), elles sont corrélées négativement
Si l’angle est proche de 90°, alors les variables ne sont pas corrélées

Show the code

factoextra::fviz_pca_var(
  res_pca,
  col.var = "cos2",
  gradient.cols = rainbow(n = 8, start = .6, end = .9),
  repel = TRUE
)

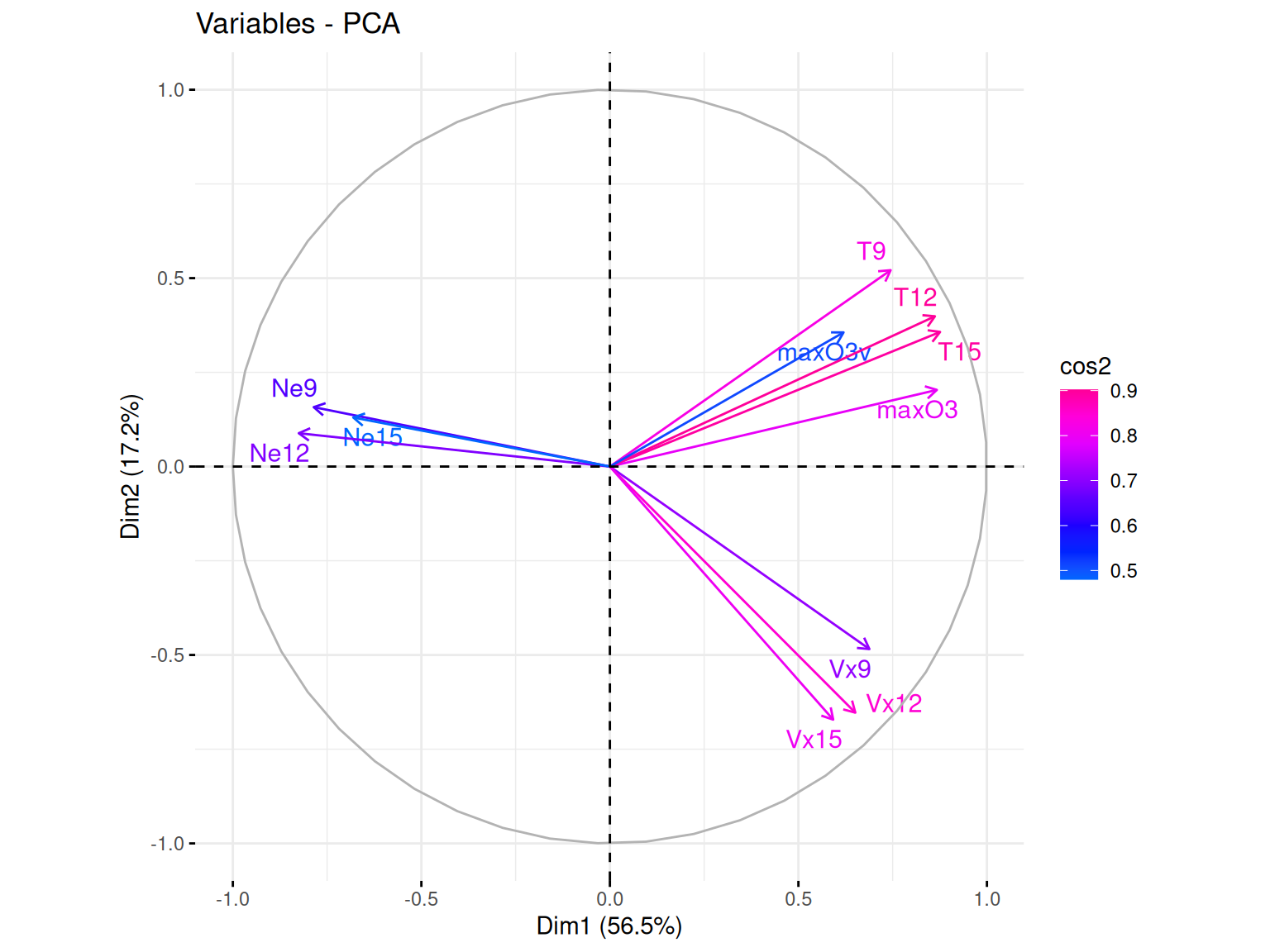
Résultats

Dans notre cas, ce que l’on peut voir c’est que la majorité de nos variables sont bien représentées par nos deux axes (cumulant plus de 70% d’explication). Mais beaucoup semblent aussi fortement corrélées avecla formation de trois groupes. Cette corrélation ayant déjà pu être observé précédemment et touours logique du fait du côté longitudinale de nos données.

Ce que l’on peut tout de même ajouté c’est que les variables max03 et surtout max03v semblent plutot corrélées aux variables température. Constat qui peut se confirmer avec le pairs.panels précédent.

Analyse inférentielle

Contrairement à la plupart des autres package R qui permettent de faire de l’apprentissage, le package glmnet n’autorise pas l’utilisation de formules. Il faut donc spécifier explicitement la matrice $X$ et le vecteur $y$.

On peut obtenir la matrice $X$ et notamment le codage des variables qualitatives avec la fonction model.matrix.

Show the code

ozone.X <- model.matrix(maxO3 ~ ., data = ozone)[, -1]
ozone.Y <- ozone$maxO3

Et ce n’est qu’après que l’on peut mettre en place la modélisation.

Ridge
Lasso

Show the code

mod.R <- glmnet(ozone.X, ozone.Y, alpha = 0)

La fonction glmnet calcule tous les estimateurs pour une grille de valeurs de $\lambda$ que l’on peut récupérer.

Show the code

mod.R$lambda %>% head()

[1] 22007.27 20052.20 18270.82 16647.69 15168.76 13821.21

Et on peut également récupérer les différentes valeurs de $\beta$ associée aux différents $\lambda$.

Show the code

beta_values <- mod.R$beta %>% as.matrix() %>% t()
rownames(beta_values) <- paste0("lambda_", seq(1, length(mod.R$lambda), by = 1))

beta_values %>% DT::datatable()

Puis on peut visualiser les chemins de régularisation des estimateurs Ridge.

Show the code

plot(mod.R, xvar = "lambda", label = TRUE)

Résultats

Ici on voit l’évolution de nos coefficients $\beta$ en fonction des diffrentes valeurs de $\lambda$. Ainsi, sur la gauche on se retrouve dans la situation où il n’y a pas de pénalisation et donc nos coefficients sont les $\beta$ de l’estimation par moindres carrés. Et donc plus $\lambda$ va augmenter, plus on se retrouvera dans une situation où les coefficients vont tendrent vers 0.

Show the code

mod.L <- glmnet(ozone.X, ozone.Y, alpha = 1)

La fonction glmnet calcule tous les estimateurs pour une grille de valeurs de $\lambda$ que l’on peut récupérer.

Show the code

mod.L$lambda %>% head()

[1] 22.00727 20.05220 18.27082 16.64769 15.16876 13.82121

Et on peut également récupérer les différentes valeurs de $\beta$ associée aux différents $\lambda$.

Show the code

beta_values <- mod.L$beta %>% as.matrix() %>% t()
rownames(beta_values) <- paste0("lambda_", seq(1, length(mod.L$lambda), by = 1))

beta_values %>% DT::datatable()

Puis on peut visualiser les chemins de régularisation des estimateurs Lasso.

Show the code

plot(mod.L, xvar = "lambda", label = TRUE)

Résultats

Selection des paramètres de régularisation

Maintenant que les modèles sont estimés avec plusieurs valeurs de $\lambda$ possibles, il se pose la question du choix du bon paramètre.
Pour cela, on utilise la fonction cv.glmnet qui, comme son nom le laisse suggérer, permet d’effectuer une validation croisée pour notre modèle avec par défaut nfolds=10 (le nombre de pli pour le découpage de sous ensembles). Puis on peut faire un plot de l’objet.

Ridge
Lasso

Show the code

ridgeCV <- cv.glmnet(ozone.X, ozone.Y, alpha = 0)
plot(ridgeCV)

On visualise ici les erreurs quadratiques calculées par validation croisée 10 blocs en fonction de $\lambda$ (échelle logarithmique). Deux traits verticaux sont représentés :

celui de gauche correspond à la valeur de $\lambda$ qui minimise l’erreur quadratique
celui de droite correspond à la plus grande valeur de $\lambda$ telle que l’erreur ne dépasse pas l’erreur minimale + 1 écart-type estimé de cette erreur

D’un point de vu pratique, cela signifie que l’utilisateur peut choisir n’importe quelle valeur de lambda entre les deux traits verticaux.
A savoir que si l’on veut diminuer la complexité du modèle on choisira la valeur de droite.

On peut obtenir ces deux valeurs assez facilement.

Show the code

cat(" Valeur minimale : ", ridgeCV$lambda.min, "\n", "Valeur maximale : ", ridgeCV$lambda.1se)

 Valeur minimale :  9.750588 
 Valeur maximale :  39.36329

Show the code

lassoCV <- cv.glmnet(ozone.X, ozone.Y, alpha = 1)
plot(lassoCV)

On visualise ici les erreurs quadratiques calculées par validation croisée 10 blocs en fonction de $\lambda$ (échelle logarithmique). Deux traits verticaux sont représentés :

celui de gauche correspond à la valeur de $\lambda$ qui minimise l’erreur quadratique
celui de droite correspond à la plus grande valeur de $\lambda$ telle que l’erreur ne dépasse pas l’erreur minimale + 1 écart-type estimé de cette erreur

On peut obtenir ces deux valeurs assez facilement.

Show the code

cat(" Valeur minimale : ", lassoCV$lambda.min, "\n", "Valeur maximale : ", lassoCV$lambda.1se)

 Valeur minimale :  1.230385 
 Valeur maximale :  4.525822

Prédiction

On souhaite maintenant prédire la variable cible pour de nouveaux individus, par exemple les 50ème et 51ème individus du jeu de données.

Une première approche pourrait consister à réajuster le modèle sur toutes les données pour la valeur de $lambda$ sélectionnée.
Cette étape est en réalité déjà effectuée par la fonction cv.glmnet. Il suffit par conséquent d’appliquer la fonction predict à l’objet obtenu avec cv.glmnet en spécifiant la valeur de $lambda$ souhaitée.

Ridge
Lasso

Show the code

predict(ridgeCV, newx = ozone.X[50:51, ], s = "lambda.min")

         lambda.min
20010723   90.10981
20010724   96.74374

Show the code

predict(ridgeCV, newx = ozone.X[50:51, ], s = "lambda.1se")

         lambda.1se
20010723   93.11072
20010724   96.26805

Show the code

predict(lassoCV, newx = ozone.X[50:51, ], s = "lambda.min")

         lambda.min
20010723   87.18235
20010724   98.23752

Show the code

predict(lassoCV, newx = ozone.X[50:51, ], s = "lambda.1se")

         lambda.1se
20010723   87.40631
20010724   95.85602

Comparaison

Puisque nous avons 3 méthodes de modélisations (MCO sans pénalisation, Ridge et Lasso), la prochaine étape logique va donc ^tre de comparer les trois méthodes pour déterminer laquelle est la plus approrié pour nos données.

On peut faire cela l’aide d’une validation croisée et pour cela on utilisera les données ozone_complet.txt qui contiennent plus d’individus et de variables.

Show the code

ozone1 <- read.table("https://lrouviere.github.io/stat_grand_dim/ozone_complet.txt", sep=";") %>%  na.omit()
ozone1.X <- model.matrix(maxO3 ~ ., data = ozone1)[, -1]
ozone1.Y <- ozone1$maxO3

Show the code

cv_ridge_vs_lasso(ozone1, fmla = formula(maxO3 ~ .)) %>% DT::datatable()

Résultats

On remarque que les approches régularisées n’apportent rien par rapport aux estimateurs MCO ici. Ceci peut s’expliquer par le fait que le nombre de variables n’est pas très important.

Pour changer, considérons toutes les interactions d’ordre 2

Show the code

cv_ridge_vs_lasso(ozone1, fmla = formula(maxO3 ~ .^2)) %>% DT::datatable()

Résultats

Les méthodes régularisées permettent ici de diminuer les erreurs quadratiques de manière intéressante. Cela vient certainement du fait du nombre de variables explicatives qui est beaucoup plus important lorsqu’on prend en compte toutes les interactions d’ordre 2.

Show the code

ozone2.X <- model.matrix(maxO3 ~ .^2, data = ozone1)[, -1]

En effet, à l’ordre 1 on est à 1366 individus pour 22 variables alors qu’à l’odre 2 on passe à 1366 individus pour 253

Conclusion

Dans cette analyse, nous avons exploré l’utilisation des méthodes Ridge et Lasso sous R.
Ces approches se révèlent particulièrement efficaces en grande dimension, offrant des solutions robustes pour la régression pénalisée.

Par la suite, le choix entre Lasso et Ridge dépend souvent des objectifs poursuivis :

Lasso intègre un mécanisme de sélection de variables, ce qui en fait un excellent outil pour identifier les prédicteurs les plus pertinents.
Ridge conserve l’ensemble des variables en réduisant leurs coefficients sans les annuler, privilégiant ainsi une approche plus réguliarisée.

(Voir la partie Rappel sur Ridge et Lasso pour plus de détails)

Session info

Show the code

sessioninfo::session_info(pkgs = "attached")

─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.4.2 (2024-10-31)
 os       Ubuntu 24.04.1 LTS
 system   x86_64, linux-gnu
 ui       X11
 language (EN)
 collate  fr_FR.UTF-8
 ctype    fr_FR.UTF-8
 tz       Europe/Paris
 date     2025-02-21
 pandoc   3.2 @ /usr/lib/rstudio/resources/app/bin/quarto/bin/tools/x86_64/ (via rmarkdown)

─ Packages ───────────────────────────────────────────────────────────────────
 package    * version date (UTC) lib source
 dplyr      * 1.1.4   2023-11-17 [1] CRAN (R 4.4.2)
 forcats    * 1.0.0   2023-01-29 [1] CRAN (R 4.4.2)
 ggplot2    * 3.5.1   2024-04-23 [1] CRAN (R 4.4.2)
 glmnet     * 4.1-8   2023-08-22 [1] CRAN (R 4.4.2)
 gridExtra  * 2.3     2017-09-09 [1] CRAN (R 4.4.2)
 kableExtra * 1.4.0   2024-01-24 [1] CRAN (R 4.4.2)
 lubridate  * 1.9.4   2024-12-08 [1] CRAN (R 4.4.2)
 Matrix     * 1.6-5   2024-01-11 [4] CRAN (R 4.3.2)
 purrr      * 1.0.2   2023-08-10 [2] CRAN (R 4.3.3)
 readr      * 2.1.5   2024-01-10 [1] CRAN (R 4.4.2)
 stringr    * 1.5.1   2023-11-14 [2] CRAN (R 4.3.3)
 tibble     * 3.2.1   2023-03-20 [2] CRAN (R 4.3.3)
 tidyr      * 1.3.1   2024-01-24 [1] CRAN (R 4.4.2)
 tidyverse  * 2.0.0   2023-02-22 [1] CRAN (R 4.4.2)

 [1] /home/clement/R/x86_64-pc-linux-gnu-library/4.4
 [2] /usr/local/lib/R/site-library
 [3] /usr/lib/R/site-library
 [4] /usr/lib/R/library

──────────────────────────────────────────────────────────────────────────────

--- title: "Exercice 06 Bonus : Ridge vs Lasso" author: "Clément Poupelin" date: "2025-02-21" date-modified: "`r Sys.Date()`" format: html: embed-resources: false toc: true code-fold: true code-summary: "Show the code" code-tools: true toc-location: right page-layout: article code-overflow: wrap toc: true number-sections: false editor: visual categories: ["Régression Ridge", "Régression Lasso", "Validation croisée"] image: "/img/gants-de-boxe.png" description: "Comparaison de la régression Ridge et Lasso via le github de Laurent Rouvière" --- Dans cette partie et avant de passer à l'exercice 7, nous allons faire la section 3.1 sur la regression Ridge et Lasso avec *`glmnet`* sous *`R`* du [tutoriel de Laurent Rouvière](https://lrouviere.github.io/TUTO_GRANDE_DIM/correction/03-ridge-lasso.html) # Rappels sur Ridge et Lasso On se base encore ici sur notre modèle classique de régression linéaire : $$y = X\beta + \mathcal{E} \quad \text{ou} \quad y = \beta_0 + \beta_1X^1 + ... + \beta_pX^p + \mathcal{E}$$ - $y \in \mathbb{R}^{n}$ la variable réponse ou variable à expliquer - $X \in \mathbb{R}^{n\times (p+1)}$ la matrice déterministe contenant nos $p$ variables explicatives - $\beta \in \mathbb{R}^{p+1}$ le vecteur qui contient les coefficients de régression $\beta_0, ..., \beta_p$ que nous cherchons à estimer - $\mathcal{E} \in \mathbb{R}^{n}$ le vecteur d'erreur qui n'est pas corrélé à nos variables explicatives. C'est la part d'aléa que nous n'arrivons pas à déterminer Pour l'estimation des coefficients de regression de ce type de modèle, nous utilisons souvent la méthodes des moindres carrées ordinaire (MCO) qui nous donne $$\hat{\beta} = \underset{\beta}{argmin}||y-X\beta||^2$$ Malheureusement, lorsque $p$ est grand ou que les variables sont linéairement dépendantes, les estimateurs des moindres carrées peuvent être mis en défaut. Les méthodes pénalisées ou sous contraintes consistent alors à restreindre l’espace sur lequel on minimise ce critère.\ L'idée principale de ces méthodes est de contraindre la valeur des estimateurs MCO pour réduire la variance, quitte à augmenter un peu le biais (d’où la terminologie de "régression biaisée"). Nous obtenons donc, pour un certain $t>0$, des estimations de la forme suivante : $$ \hat{\beta}^{pen} = \underset{\beta}{argmin}||y-X\beta||^2 \quad \text{sous la contrainte} \quad ||\beta||? \leq t$$ ::: panel-tabset ## Ridge La régression Ridge contraint la **norme** $\ell^2$ des coefficients $\beta$ à ne pas exploser, i.e $||\beta||_2 = \sum_{j=0}^{p} \beta_j^2 \leq t$. Cela conduit à la solution d'optimisation suivante : $$ \hat{\beta}_{Ridge} = \underset{\beta}{\operatorname{argmin}} \ ||y - X\beta||^2 \quad \text{sous la contrainte} \quad \sum_{j=0}^{p} \beta_j^2 \leq t $$ où $\hat{\beta}_{Ridge}$ est **unique**, contrairement à Lasso qui peut produire plusieurs solutions. Contrairement à Lasso, Ridge ne met pas exactement à zéro certains coefficients, mais réduit leur valeur. Il n'y a donc pas de sélection de variable effectué.\ Cette méthode est tout de même robuste en grande dimension et particulièrement utile lorsque les variables sont fortement corrélées. Il empêche les coefficients de devenir trop grands, ce qui réduit la variance du modèle.\ ## Lasso La régression Lasso (pour Least Absolute Shrinkage and Selection Operator) contraint la norme $\ell^1$ de $\beta$ à ne pas exploser, i.e $||\beta||_1 = \sum_{j=0}^{p} |\beta_j| \leq t$. Nous obtenons donc $$\hat{\beta}_{Lasso} = \underset{\beta}{argmin}||y-X\beta||^2 \quad \text{sous la contrainte} \quad \sum_{j=0}^{p} |\beta_j| \leq t $$ Où $\hat{\beta}_{Lasso}$ n’est pas nécessairement unique mais la prévision $\hat{y} = X\hat{\beta}_{Lasso}$ est unique.\ Cette méthode est principalement caractérisée par le fait qu'elle est robuste à la grande dimension en sélectionnant les variables les plus pertinentes. En effet, elle nous permet de réduire les coefficients MCO des variables sélectionnées en rapprochant leur valeur de 0, ce qui est appelé la propriété de "seuillage doux" du Lasso. ::: Ici, il sera donc présenté les étapes principales qui permettent de faire ce type de régression avec *`R`*. Le package le plus souvent utilisé est *`glmnet`*. # Setup :::: panel-tabset ## Packages ```{r, warning=FALSE, message=FALSE} # Inférence library(glmnet) ## regression pénalisée # Plots ## ggplot library(ggplot2) library(gridExtra) ``` ## Fonctions ::: panel-tabset ### boxplot ```{r} my_boxplot <- function(data) { data_long <- reshape2::melt(data) ggplot(data_long, aes(x = variable, y = value, fill = variable)) + geom_boxplot() + scale_fill_viridis_d() + # Palette de couleurs harmonieuse labs(title = "Distribution des Variables (Boxplot)", x = "Variables", y = "Valeurs") + theme_minimal() + # Thème épuré theme(axis.text.x = element_text(angle = 45, hjust = 1)) # Rotation des étiquettes } ``` ### pairs.panels ```{r} my_pairs.panels <- function(data) { psych::pairs.panels( data, method = "pearson", # Méthode de corrélation hist.col = RColorBrewer::brewer.pal(9, "Set3"), # Couleurs des histogrammes density = TRUE, # Ajout des courbes de densité ellipses = TRUE, # Ajout d'ellipses smooth = TRUE, # Ajout de régressions lissées lm = TRUE, # Ajout des droites de régression col = "#69b3a2", # Couleur des points alpha = 0.5 # Transparence ) } ``` ### Comparaison de modèles ```{r} cv_ridge_vs_lasso <- function(data, fmla) { set.seed(140400) data.X <- model.matrix(fmla, data = data)[, -1] data.Y <- data$maxO3 blocs <- caret::createFolds(1:nrow(data), k = 10) prev <- matrix(0, ncol = 3, nrow = nrow(data)) %>% as.data.frame() names(prev) <- c("Linéaire (MCO)", "Ridge", "Lasso") for (k in 1:10) { app <- data[-blocs[[k]], ] test <- data[blocs[[k]], ] app.X <- data.X[-blocs[[k]], ] app.Y <- data.Y[-blocs[[k]]] test.X <- data.X[blocs[[k]], ] test.Y <- data.Y[blocs[[k]]] ridge <- cv.glmnet(app.X, app.Y, alpha = 0) lasso <- cv.glmnet(app.X, app.Y, alpha = 1) lin <- lm(fmla, data = app) prev[blocs[[k]], ] <- tibble::tibble( lin = predict(lin, newdata = test), ridge = as.vector(predict(ridge, newx = test.X)), lasso = as.vector(predict(lasso, newx = test.X)) ) } err <- prev %>% mutate(obs = data$maxO3) %>% summarise_at(1:3, ~ mean((obs - .)^2)) return(err) } ``` ::: :::: # Données On considère le jeu de données *ozone.txt* où on cherche à expliquer la concentration maximale en ozone relevée sur une journée (variable *maxO3*) par d’autres variables essentiellement météorologiques. La base de données d'origine *ozone.txt* répertorie ainsi 112 données météorologiques mesurées durant l'été 2001 à Rennes. Celles-ci sont caractérisées par les 13 variables suivantes : ```{r, echo=FALSE, message=FALSE, warning=FALSE} ozone <-read.table("https://r-stat-sc-donnees.github.io/ozone.txt", header=TRUE) library(tidyverse) library(kableExtra) identity_keys <- cell_spec( x = colnames(ozone), format = "html", bold = TRUE) identity_values <- c("concentration maximale d'ozone (en DU)", "température à 9H (en °C)", "température à 12H (en °C)", "température à 15H (en °C)", "nébulosité à 9H (en octa)", "nébulosité à 12H (en octa)", "nébulosité à 15H (en octa)", "vitesse du vent à 9H", "vitesse du vent à 12H", "vitesse du vent à 15H", "concentration maximale d'ozone de la veille (en DU)", "direction principale du vent (Nord / Ouest / Sud / Est)", "présence ou non de pluie (Sec / Pluie)") tibble( keys = identity_keys, values = identity_values, ) %>% kbl( format = "html", booktabs = TRUE, escape = FALSE, col.names = NULL ) %>% kable_styling(bootstrap_options = c("hover", "condensed")) ``` On identifie le regroupement de toutes les données météorologiques récoltées en une journée par la date à laquelle les relevés ont été effectués. ```{r} ozone <-read.table("https://r-stat-sc-donnees.github.io/ozone.txt", header=TRUE) ozone %>% DT::datatable() ``` ::: callout-note Bien évidémment on a vérifié qu'il n'y a pas de valeurs manquantes dans cette base de données avec la fonction *`anyNA`* qui renvoie `r anyNA(ozone)` ::: # Analyse descriptive ::::::::::::::::::::: panel-tabset ## Boxplot On peut regarder un peu la distribution de nos différents variables quantitatives via des boxplots. ```{r, message=FALSE, fig.height=6, fig.width=8} my_boxplot(ozone) ``` :::: success-header ::: success-icon ::: Résultats :::: ::: success On remarque bien que les variabeles qui sont de même nature mais à des points de temps différents sont d'avantages similaires. ::: Pour confirmer cela, on peut faire des boxplot pour uniquement une varibale et ses différents points de temps. ::: panel-tabset ### Température ```{r, message=FALSE, fig.height=6, fig.width=8} subset(ozone, select = c("T9", "T12", "T15")) %>% my_boxplot() ``` ### Nébulosité ```{r, message=FALSE, fig.height=6, fig.width=8} subset(ozone, select = c("Ne9", "Ne12", "Ne15")) %>% my_boxplot() ``` ### Vitesse du vent ```{r, message=FALSE, fig.height=6, fig.width=8} subset(ozone, select = c("Vx9", "Vx12", "Vx15")) %>% my_boxplot() ``` ::: ## Correlation On regarde ici la corrélation calculée entre chacune de nos variables. ```{r, fig.height=22, fig.width=28} my_pairs.panels(ozone) ``` :::: success-header ::: success-icon ::: Résultats :::: ::: success On voit la présence de plusieurs fortes corrélations qui peut déjà nous alerter si l'on veut faire des modèles de regressions linéaires car on risque d'avoir un problème de colinéarité entre les varibales explicatives. Cependant ces corrélation fortes sont surtout présentes pour les variables qui sont à différents points de temps ce qui est logique. ::: ## PCA Avec une Analyse en Composantes Principales (PCA) on peut regarder un peu le comportement de nos données. En effet, Cette méthode respose sur la transformation des variables d'origine en nouvelles variables non corrélées, appelées composantes principales, qui capturent successivement la plus grande variance possible des données. ```{r} res_pca <- FactoMineR::PCA( ozone, quali.sup = c(which(colnames(ozone) %in% c("vent", "pluie"))), quanti.sup = c(which(colnames(ozone) %in% c("max03", "max03v"))), graph = FALSE ) ``` Ici, on spécifi nos varibales qualitatives et on décide de mettre la variable *max03* et *max03v* en variable supplémentaire, ce qui veut d'ire qu'elles ne seront pas considérés pour la formation de nos composantes principales (variable que l'on cherchera à estimer plus tard). ::::::::::::: panel-tabset #### Barplot des variances Tout d'abord, on peut commencer par regarder le pourcentage de variance expliqué par nos différentes composantes principales. ```{r} factoextra::fviz_eig( res_pca, ncp = 10, addlabels = TRUE, barfill = "coral", barcolor = "coral", ylim = c(0, 60), main = "Percentage of variance of the 10 first components" ) ``` :::: success-header ::: success-icon ::: Résultats :::: ::: success On voit ainsi que la majorité de la variance est expliquée par nos deux premières composantes principales. ::: #### Individus Le plan des individus est une projection des observations sur les axes principaux de la PCA. Cette visualisation permet d’identifier des regroupements, tendances et anomalies au sein des données. Ainsi, des individus proches sur le graphique ont des caractéristiques similaires par rapport aux variables utilisées. Puis, le placement d'un individu en fonction des axes peut permettre de savoir comment le jouer se caractérise par rapport aux variables qui contribuent le plus à ces axes. ::: panel-tabset ##### Pluie ```{r, fig.height=6, fig.width=8} factoextra::fviz_pca_ind( res_pca, label = "none", pointsize = 2, habillage = as.factor(ozone$pluie), addEllipses = TRUE, ellipse.level = 0.95 ) ``` ##### vent ```{r, fig.height=6, fig.width=8} factoextra::fviz_pca_ind( res_pca, label = "none", pointsize = 2, habillage = as.factor(ozone$vent), addEllipses = TRUE, ellipse.level = 0.95 ) ``` ::: :::: success-header ::: success-icon ::: Résultats :::: ::: success Ici on voit une repartition plutot uniforme sur le plan qui ne semble pas permettre de distinguer une séparation forte correspodant à nos variables qualitatives. ::: #### Variables Le cercle des variables est une représentation graphique qui permet d’analyser les relations entre les variables initiales et les composantes principales qui forment nos axes. Il est basé sur les corrélations entre les variables et les axes principaux. Ainsi, plus une variable est proche du bord du cercle, plus elle est bien représentée sur le plan factoriel et contribue fortement à la formation des axes. Ici, on utilise le cos2 pour le gradient de couleur qui va aider à l'indentifictation de ces différentes qualitées de représentation. De plus, selon l'angle entre deux varibles, on peut faire des suppositions sur leur corrélation : - Si deux variables ont des vecteurs proches (petit angle), elles sont fortement corrélées positivement - Si deux variables ont des vecteurs opposés (angle proche de 180°), elles sont corrélées négativement - Si l’angle est proche de 90°, alors les variables ne sont pas corrélées ```{r, fig.height=6, fig.width=8} factoextra::fviz_pca_var( res_pca, col.var = "cos2", gradient.cols = rainbow(n = 8, start = .6, end = .9), repel = TRUE ) ``` :::: success-header ::: success-icon ::: Résultats :::: ::: success Dans notre cas, ce que l'on peut voir c'est que la majorité de nos variables sont bien représentées par nos deux axes (cumulant plus de 70% d'explication). Mais beaucoup semblent aussi fortement corrélées avecla formation de trois groupes. Cette corrélation ayant déjà pu être observé précédemment et touours logique du fait du côté longitudinale de nos données. Ce que l'on peut tout de même ajouté c'est que les variables max03 et surtout max03v semblent plutot corrélées aux variables température. Constat qui peut se confirmer avec le pairs.panels précédent. ::: ::::::::::::: ::::::::::::::::::::: # Analyse inférentielle Contrairement à la plupart des autres package *`R`* qui permettent de faire de l’apprentissage, le package *`glmnet`* n’autorise pas l’utilisation de formules. Il faut donc spécifier explicitement la matrice $X$ et le vecteur $y$.\ On peut obtenir la matrice $X$ et notamment le codage des variables qualitatives avec la fonction *`model.matrix`*. ```{r} ozone.X <- model.matrix(maxO3 ~ ., data = ozone)[, -1] ozone.Y <- ozone$maxO3 ``` Et ce n'est qu'après que l'on peut mettre en place la modélisation. ::::::::: panel-tabset ## Ridge ```{r} mod.R <- glmnet(ozone.X, ozone.Y, alpha = 0) ``` La fonction *`glmnet`* calcule tous les estimateurs pour une grille de valeurs de $\lambda$ que l'on peut récupérer. ```{r} mod.R$lambda %>% head() ``` Et on peut également récupérer les différentes valeurs de $\beta$ associée aux différents $\lambda$. ```{r} beta_values <- mod.R$beta %>% as.matrix() %>% t() rownames(beta_values) <- paste0("lambda_", seq(1, length(mod.R$lambda), by = 1)) beta_values %>% DT::datatable() ``` Puis on peut visualiser les chemins de régularisation des estimateurs **Ridge**. ```{r} plot(mod.R, xvar = "lambda", label = TRUE) ``` :::: success-header ::: success-icon ::: Résultats :::: ::: success Ici on voit l'évolution de nos coefficients $\beta$ en fonction des diffrentes valeurs de $\lambda$. Ainsi, sur la gauche on se retrouve dans la situation où il n'y a pas de pénalisation et donc nos coefficients sont les $\beta$ de l'estimation par moindres carrés. Et donc plus $\lambda$ va augmenter, plus on se retrouvera dans une situation où les coefficients vont tendrent vers 0. ::: ## Lasso ```{r} mod.L <- glmnet(ozone.X, ozone.Y, alpha = 1) ``` La fonction *`glmnet`* calcule tous les estimateurs pour une grille de valeurs de $\lambda$ que l'on peut récupérer. ```{r} mod.L$lambda %>% head() ``` Et on peut également récupérer les différentes valeurs de $\beta$ associée aux différents $\lambda$. ```{r} beta_values <- mod.L$beta %>% as.matrix() %>% t() rownames(beta_values) <- paste0("lambda_", seq(1, length(mod.L$lambda), by = 1)) beta_values %>% DT::datatable() ``` Puis on peut visualiser les chemins de régularisation des estimateurs **Lasso**. ```{r} plot(mod.L, xvar = "lambda", label = TRUE) ``` :::: success-header ::: success-icon ::: Résultats :::: ::: success Ici on voit l'évolution de nos coefficients $\beta$ en fonction des diffrentes valeurs de $\lambda$. Ainsi, sur la gauche on se retrouve dans la situation où il n'y a pas de pénalisation et donc nos coefficients sont les $\beta$ de l'estimation par moindres carrés. Et donc plus $\lambda$ va augmenter, plus on se retrouvera dans une situation où les coefficients vont tendrent vers 0. ::: ::::::::: # Selection des paramètres de régularisation Maintenant que les modèles sont estimés avec plusieurs valeurs de $\lambda$ possibles, il se pose la question du choix du bon paramètre.\ Pour cela, on utilise la fonction *`cv.glmnet`* qui, comme son nom le laisse suggérer, permet d'effectuer une validation croisée pour notre modèle avec par défaut *`nfolds=10`* (le nombre de pli pour le découpage de sous ensembles). Puis on peut faire un *`plot`* de l’objet. ::: panel-tabset ## Ridge ```{r} ridgeCV <- cv.glmnet(ozone.X, ozone.Y, alpha = 0) plot(ridgeCV) ``` On visualise ici les erreurs quadratiques calculées par validation croisée 10 blocs en fonction de $\lambda$ (échelle logarithmique). Deux traits verticaux sont représentés : - celui de gauche correspond à la valeur de $\lambda$ qui minimise l’erreur quadratique - celui de droite correspond à la plus grande valeur de $\lambda$ telle que l’erreur ne dépasse pas l’erreur minimale + 1 écart-type estimé de cette erreur D’un point de vu pratique, cela signifie que l’utilisateur peut choisir n’importe quelle valeur de lambda entre les deux traits verticaux.\ A savoir que si l'on veut diminuer la complexité du modèle on choisira la valeur de droite. On peut obtenir ces deux valeurs assez facilement. ```{r} cat(" Valeur minimale : ", ridgeCV$lambda.min, "\n", "Valeur maximale : ", ridgeCV$lambda.1se) ``` ## Lasso ```{r} lassoCV <- cv.glmnet(ozone.X, ozone.Y, alpha = 1) plot(lassoCV) ``` On visualise ici les erreurs quadratiques calculées par validation croisée 10 blocs en fonction de $\lambda$ (échelle logarithmique). Deux traits verticaux sont représentés : - celui de gauche correspond à la valeur de $\lambda$ qui minimise l’erreur quadratique - celui de droite correspond à la plus grande valeur de $\lambda$ telle que l’erreur ne dépasse pas l’erreur minimale + 1 écart-type estimé de cette erreur D’un point de vu pratique, cela signifie que l’utilisateur peut choisir n’importe quelle valeur de lambda entre les deux traits verticaux.\ A savoir que si l'on veut diminuer la complexité du modèle on choisira la valeur de droite. On peut obtenir ces deux valeurs assez facilement. ```{r} cat(" Valeur minimale : ", lassoCV$lambda.min, "\n", "Valeur maximale : ", lassoCV$lambda.1se) ``` ::: # Prédiction On souhaite maintenant prédire la variable cible pour de nouveaux individus, par exemple les 50ème et 51ème individus du jeu de données. Une première approche pourrait consister à réajuster le modèle sur toutes les données pour la valeur de $lambda$ sélectionnée.\ Cette étape est en réalité déjà effectuée par la fonction *`cv.glmnet`*. Il suffit par conséquent d’appliquer la fonction predict à l’objet obtenu avec *`cv.glmnet`* en spécifiant la valeur de $lambda$ souhaitée. ::: panel-tabset ## Ridge ```{r} predict(ridgeCV, newx = ozone.X[50:51, ], s = "lambda.min") ``` ```{r} predict(ridgeCV, newx = ozone.X[50:51, ], s = "lambda.1se") ``` ## Lasso ```{r} predict(lassoCV, newx = ozone.X[50:51, ], s = "lambda.min") ``` ```{r} predict(lassoCV, newx = ozone.X[50:51, ], s = "lambda.1se") ``` ::: # Comparaison Puisque nous avons 3 méthodes de modélisations (MCO sans pénalisation, Ridge et Lasso), la prochaine étape logique va donc \^tre de comparer les trois méthodes pour déterminer laquelle est la plus approrié pour nos données.\ On peut faire cela l’aide d’une validation croisée et pour cela on utilisera les données *ozone_complet.txt* qui contiennent plus d’individus et de variables. ```{r} ozone1 <- read.table("https://lrouviere.github.io/stat_grand_dim/ozone_complet.txt", sep=";") %>% na.omit() ozone1.X <- model.matrix(maxO3 ~ ., data = ozone1)[, -1] ozone1.Y <- ozone1$maxO3 ``` ```{r} cv_ridge_vs_lasso(ozone1, fmla = formula(maxO3 ~ .)) %>% DT::datatable() ``` :::: success-header ::: success-icon ::: Résultats :::: ::: success On remarque que les approches régularisées n’apportent rien par rapport aux estimateurs MCO ici. Ceci peut s’expliquer par le fait que le nombre de variables n’est pas très important. ::: Pour changer, considérons toutes les interactions d’ordre 2 ```{r} cv_ridge_vs_lasso(ozone1, fmla = formula(maxO3 ~ .^2)) %>% DT::datatable() ``` :::: success-header ::: success-icon ::: Résultats :::: ::: success Les méthodes régularisées permettent ici de diminuer les erreurs quadratiques de manière intéressante. Cela vient certainement du fait du nombre de variables explicatives qui est beaucoup plus important lorsqu’on prend en compte toutes les interactions d’ordre 2. ```{r} ozone2.X <- model.matrix(maxO3 ~ .^2, data = ozone1)[, -1] ``` En effet, à l'ordre 1 on est à `r dim(ozone1.X)[1]` individus pour `r dim(ozone1.X)[2]` variables alors qu'à l'odre 2 on passe à `r dim(ozone2.X)[1]` individus pour `r dim(ozone2.X)[2]` ::: # Conclusion Dans cette analyse, nous avons exploré l’utilisation des méthodes **Ridge** et **Lasso** sous *`R`*.\ Ces approches se révèlent particulièrement efficaces en grande dimension, offrant des solutions robustes pour la régression pénalisée. Par la suite, le choix entre **Lasso** et **Ridge** dépend souvent des objectifs poursuivis : - **Lasso** intègre un mécanisme de sélection de variables, ce qui en fait un excellent outil pour identifier les prédicteurs les plus pertinents. - **Ridge** conserve l’ensemble des variables en réduisant leurs coefficients sans les annuler, privilégiant ainsi une approche plus réguliarisée. (Voir la partie **Rappel sur Ridge et Lasso** pour plus de détails) # Session info ```{r} sessioninfo::session_info(pkgs = "attached") ```