Exercice 4

Utilisation des précédentes techniques de selections de variable et de validation croisée dans le cadre de données de grandes dimension avec le jeu de données Caravan
TP
Author

Clément Poupelin

Published

February 20, 2025

Setup

Show the code 
# Données
library(ISLR)         # Caravan data 
library(dplyr)        # manipulation des données


library(car)          # pour VIF





# Plots
## ggplot
library(ggplot2)
library(gridExtra)
Show the code 
my_boxplot <- function(data) {
  # Transformer les données en format long pour ggplot
  data_long <- reshape2::melt(data)
  
  ggplot(data_long, aes(x = variable, y = value, fill = variable)) +
    geom_boxplot() +
    scale_fill_viridis_d() +  # Palette de couleurs harmonieuse
    labs(title = "Distribution des Variables (Boxplot)", x = "Variables", y = "Valeurs") +
    theme_minimal() +  # Thème épuré
    theme(axis.text.x = element_text(angle = 45, hjust = 1))  # Rotation des étiquettes
}
Show the code 
my_VIFplot <- function(vif) {
  vif_df <- data.frame(Variable = names(vif), VIF = vif)
  
  p <- ggplot(vif_df, aes(
    x = reorder(Variable, VIF),
    y = pmin(VIF, 15),
    fill = VIF > 10
  )) +
    geom_bar(stat = "identity") +
    geom_text(aes(label = ifelse(VIF > 10, round(VIF, 1), "")), hjust = -0.2, size = 6) +
    coord_flip() +
    scale_fill_manual(values = c("FALSE" = "#0072B2", "TRUE" = "#D55E00")) +
    labs(title = "Variance Inflation Factor (VIF)", x = "Variables", y = "VIF (limité à 15)") +
    theme_minimal() +
    theme(
      axis.title = element_text(size = 34, face = "bold"),
      plot.title = element_text(
        size = 54,
        face = "bold",
        hjust = 0.5
      ),
      axis.text.x = element_text(size = 26),
      axis.text.y = element_text(size = 18),
      legend.text = element_text(size = 30),
      legend.title = element_text(size = 38, face = "bold")
    )
  
  return(p)
}

Données

On considère le jeu de données Caravan de la librairie ISLR de R. Ce jeu de données contient, pour 5822 clients d’une assurance, 86 variables décrivant leur profil.
Dans ces 86 variables, les variables 1 à 43 contiennent des données sociodémographiques et les variables 44 à 86 la propriété du produit.
A savoir que les données sociodémographiques sont dérivées des codes postaux. Tous les clients vivant dans des zones ayant le même code postal ont les mêmes attributs sociodémographiques.

Puis, la dernière variable Purchase indique si le client a souscrit une assurance pour caravane ou non. Cela veut donc dire que nos variables sont pour beaucoup qualitative (nominales ou ordinales).

Les détails sur l’information représentée par nos différentes variables se trouvent sur cette page. Le détail ne sera donc pas afficher ici car un peu trop long mais je vous invite à jeter un oeil pour mieux comprendre les données.

Aussi, à la vu des dimensions, on se passera d’afficher le summary(). Mais n’oublions pas de vérifier s’il y a des valeurs manquantes.

Show the code 
cat("Y-at-il des valeurs manquantes : ", anyNA(Caravan))
Y-at-il des valeurs manquantes :  FALSE

Pour nos analyses, on s’intéressera à la variable Purchase. Celle ci pouvans déjà nous indiquer que le pourcentage de clients ayant souscrit à une assurance caravane est de 5.98%

Analyse descriptive (pertinent ?? car var quali)

On peut regarder un peu la distribution de nos différents variables quantitatives via des boxplots.

Show the code 
my_boxplot(Caravan)

Résultats

On voit que pour nos variables, nous sommes sur des valeurs généralement comprises entre 0 et 10 sauf pour la vairiable MOSTYPE représentant ??? qui a des valuers beaucoup plus importante.

Ainsi, ssi l’on veut mieux voir la distribution de nos variables, on peut enlever MOSTYPE.

Show the code 
my_boxplot(Caravan[,-1])

Lorsque nos données sont de grandes dimension, des correlation panel deviennent difficile à produire et à lire. On peut donc tenter de passer sur une représentation commune qui est la heatmap. Ici, on fera la heatmap pour nos variable sociodémographiques, pour nos variables de propriété du produit et sur toutes les vaiables.

Show the code 
data_subset <- Caravan[,1:43]
data_long <- reshape2::melt(as.matrix(data_subset))

ggplot(data_long, aes(x = Var2, y = Var1, fill = value)) +
  geom_tile() +
  scale_fill_gradient(low = "white", high = "blue") +  
  labs(title = "Heatmap des 43 premières variables de Caravan",
       x = "Variables",
       y = "Observations") +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 90, hjust = 1))

Résultats

Résultats

Résultats

Avec une Analyse en Composantes Principales (PCA) on peut regarder un peu le comportement de nos données.

En effet, Cette méthode respose sur la transformation des variables d’origine en nouvelles variables non corrélées, appelées composantes principales, qui capturent successivement la plus grande variance possible des données.

Show the code 
res_pca <- FactoMineR::PCA(Caravan, 
                           quali.sup = c(which(colnames(Caravan) %in% c("Purchase"))),
                           graph = FALSE)

Ici, on spécifi notre variable qualitative en variable supplémentaire, ce qui veut dire qu’elles ne seront pas considérés pour la formation de nos composantes principales (variable que l’on cherchera à estimer plus tard).

Tout d’abord, on peut commencer par regarder le pourcentage de variance expliqué par nos différentes composantes principales.

Show the code 
factoextra::fviz_eig(
  res_pca,
  ncp = 15,
  addlabels = TRUE,
  barfill = "coral",
  barcolor = "coral",
  ylim = c(0, 15),
  main = "Percentage of variance of the 15 first components"
)

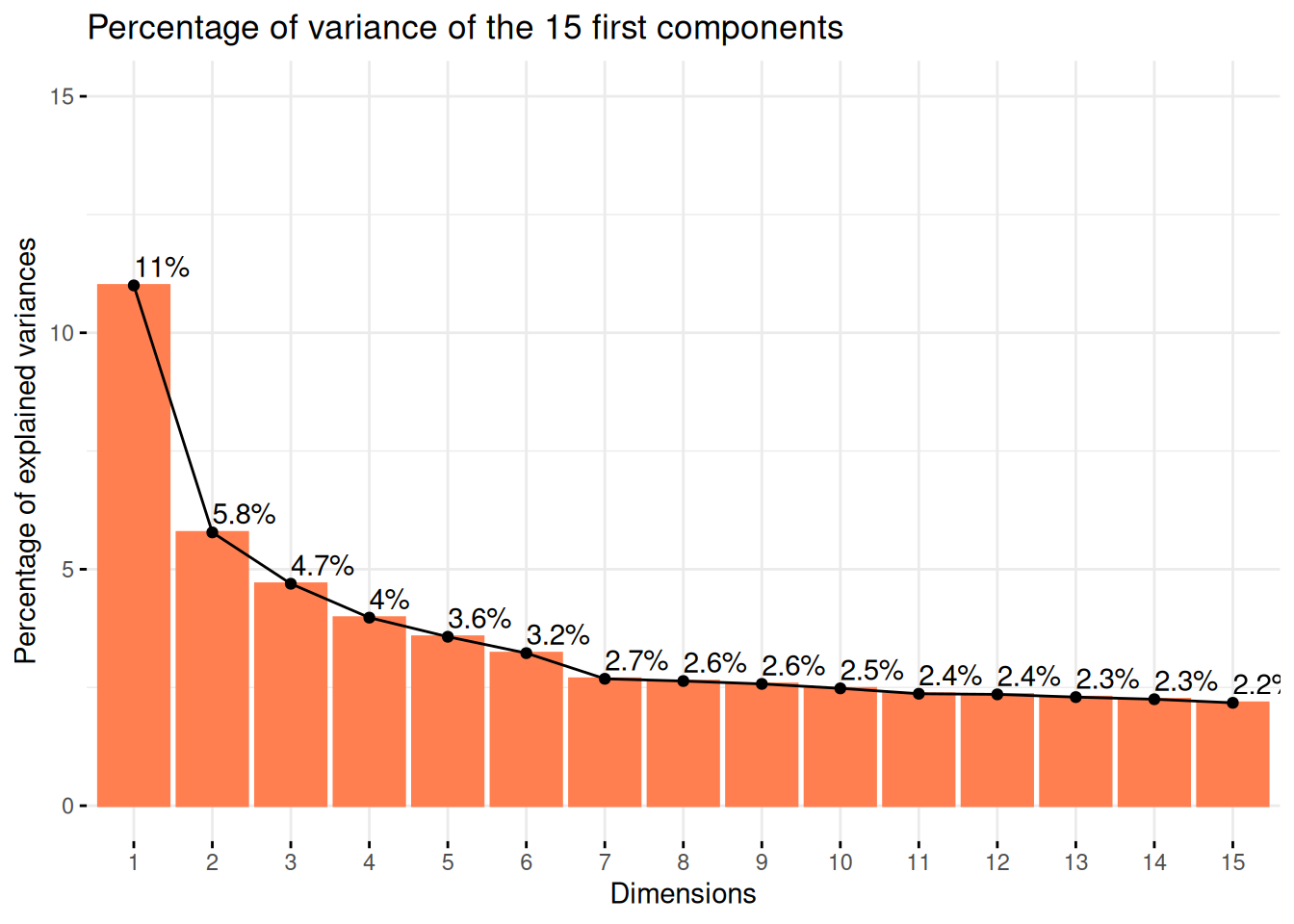
Résultats

On voit ainsi que la variance expliqué par nos deux premiers axes est d’environ 16%. Ce qui est une situation que l’on peut facilement retrouver dans des cas de grandes dimensions avec beaucoup de variables.

Le plan des individus est une projection des observations sur les axes principaux de la PCA. Cette visualisation permet d’identifier des regroupements, tendances et anomalies au sein des données.

Ainsi, des individus proches sur le graphique ont des caractéristiques similaires par rapport aux variables utilisées.

Puis, le placement d’un individu en fonction des axes peut permettre de savoir comment le jouer se caractérise par rapport aux variables qui contribuent le plus à ces axes.

Show the code 
factoextra::fviz_pca_ind(
  res_pca,
  label = "none",
  pointsize = 2,
  habillage = as.factor(Caravan$Purchase),
  addEllipses = TRUE,
  ellipse.level = 0.95
)

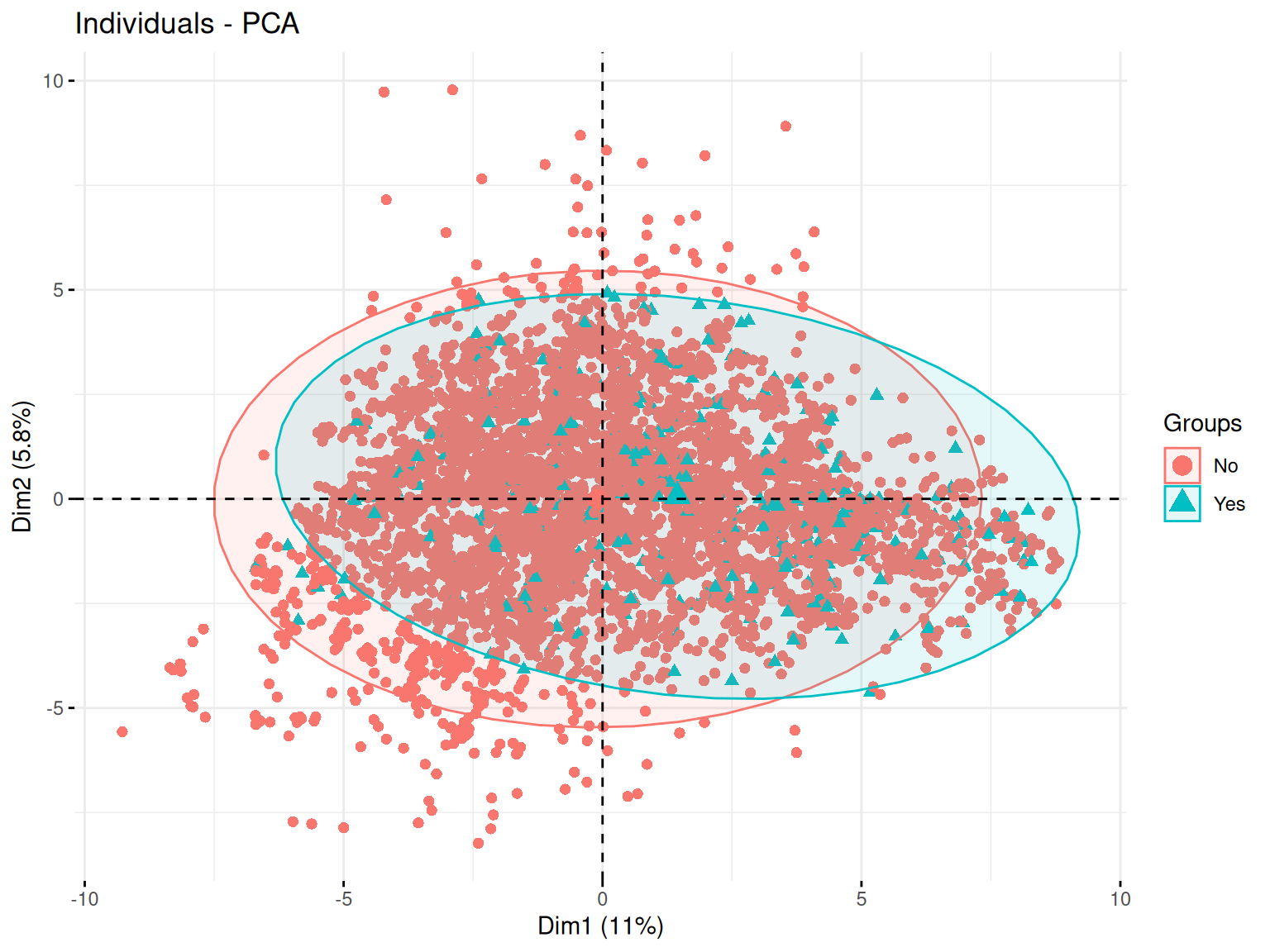
Résultats

Ici on voit une repartition plutot uniforme sur le plan qui ne semble pas permettre de distinguer une séparation forte correspodant à notre variable qualitative.

Le cercle des variables est une représentation graphique qui permet d’analyser les relations entre les variables initiales et les composantes principales qui forment nos axes. Il est basé sur les corrélations entre les variables et les axes principaux.

Ainsi, plus une variable est proche du bord du cercle, plus elle est bien représentée sur le plan factoriel et contribue fortement à la formation des axes. Ici, on utilise le cos2 pour le gradient de couleur qui va aider à l’indentifictation de ces différentes qualitées de représentation.

De plus, selon l’angle entre deux varibles, on peut faire des suppositions sur leur corrélation :

  • Si deux variables ont des vecteurs proches (petit angle), elles sont fortement corrélées positivement

  • Si deux variables ont des vecteurs opposés (angle proche de 180°), elles sont corrélées négativement

  • Si l’angle est proche de 90°, alors les variables ne sont pas corrélées

Show the code 
factoextra::fviz_pca_var(
  res_pca,
  col.var = "cos2",
  gradient.cols = rainbow(n = 8, start = .6, end = .9),
  repel = TRUE
)

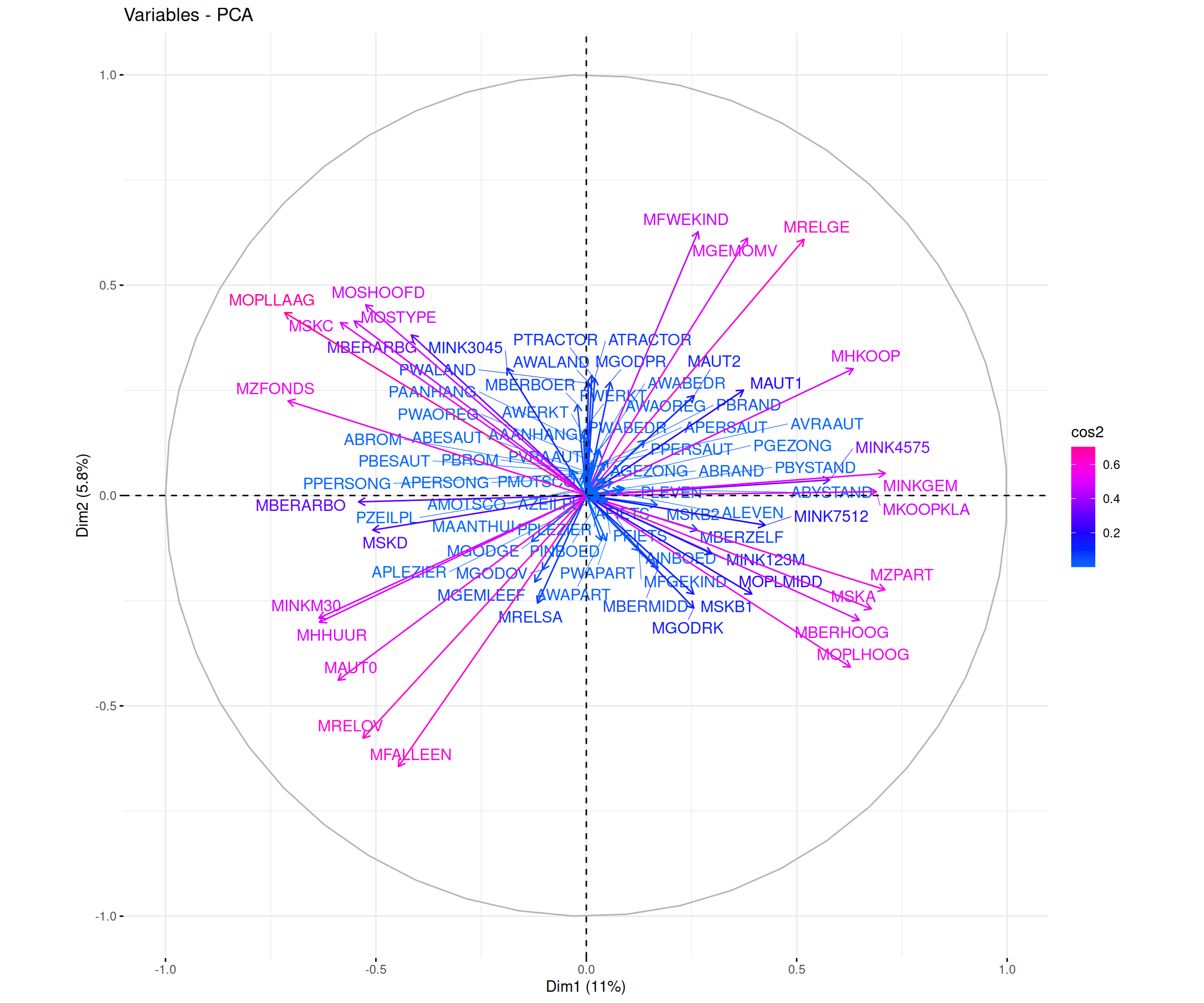
Résultats

Ici aussi, du fait du grand nombre de variable il est difficile de dicerner quelque chose de pertinent.

Maintenant, certaines variables sont tout de même bien représenter sur nos premiers axes et sont assez proche, ce qui témoigne d’une corrélation entre elles.

Analyse inférentielle

Modèle brut

Ajustons un modèle de régression logistique modélisant la probabilité de souscrire une assurance caravane en fonction de toutes les autres variables à disposition

Show the code 
mod1 <- glm(Caravan$Purchase~.,
                family = binomial,
                Caravan)
Warning: glm.fit: des probabilités ont été ajustées numériquement à 0 ou 1
Show the code 
mod1 %>% summary()

Call:
glm(formula = Caravan$Purchase ~ ., family = binomial, data = Caravan)

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)  2.542e+02  1.116e+04   0.023  0.98183    
MOSTYPE      6.580e-02  4.624e-02   1.423  0.15468    
MAANTHUI    -1.832e-01  1.927e-01  -0.951  0.34157    
MGEMOMV     -2.696e-02  1.399e-01  -0.193  0.84723    
MGEMLEEF     2.096e-01  1.016e-01   2.063  0.03911 *  
MOSHOOFD    -2.767e-01  2.076e-01  -1.333  0.18247    
MGODRK      -1.142e-01  1.069e-01  -1.068  0.28535    
MGODPR      -1.910e-02  1.177e-01  -0.162  0.87112    
MGODOV      -1.618e-02  1.055e-01  -0.153  0.87818    
MGODGE      -6.817e-02  1.113e-01  -0.612  0.54024    
MRELGE       2.310e-01  1.566e-01   1.475  0.14031    
MRELSA       8.509e-02  1.466e-01   0.580  0.56169    
MRELOV       1.467e-01  1.562e-01   0.939  0.34759    
MFALLEEN    -8.291e-02  1.311e-01  -0.633  0.52702    
MFGEKIND    -1.154e-01  1.337e-01  -0.863  0.38813    
MFWEKIND    -8.140e-02  1.417e-01  -0.575  0.56561    
MOPLHOOG     9.717e-04  1.311e-01   0.007  0.99408    
MOPLMIDD    -9.077e-02  1.365e-01  -0.665  0.50605    
MOPLLAAG    -1.994e-01  1.376e-01  -1.449  0.14740    
MBERHOOG     8.883e-02  9.349e-02   0.950  0.34204    
MBERZELF     3.918e-02  9.897e-02   0.396  0.69219    
MBERBOER    -1.169e-01  1.104e-01  -1.059  0.28951    
MBERMIDD     1.353e-01  9.191e-02   1.472  0.14106    
MBERARBG     3.976e-02  9.067e-02   0.438  0.66104    
MBERARBO     9.954e-02  9.143e-02   1.089  0.27628    
MSKA         2.690e-02  1.035e-01   0.260  0.79502    
MSKB1       -8.801e-03  1.011e-01  -0.087  0.93064    
MSKB2        1.200e-02  9.081e-02   0.132  0.89485    
MSKC         9.016e-02  9.958e-02   0.905  0.36527    
MSKD        -2.468e-02  9.724e-02  -0.254  0.79967    
MHHUUR      -1.472e+01  8.140e+02  -0.018  0.98557    
MHKOOP      -1.469e+01  8.140e+02  -0.018  0.98561    
MAUT1        1.819e-01  1.514e-01   1.202  0.22953    
MAUT2        1.507e-01  1.371e-01   1.099  0.27162    
MAUT0        9.325e-02  1.436e-01   0.649  0.51603    
MZFONDS     -1.445e+01  9.359e+02  -0.015  0.98768    
MZPART      -1.451e+01  9.359e+02  -0.016  0.98763    
MINKM30      1.181e-01  1.006e-01   1.174  0.24039    
MINK3045     1.366e-01  9.650e-02   1.415  0.15694    
MINK4575     1.009e-01  9.667e-02   1.043  0.29678    
MINK7512     1.144e-01  1.027e-01   1.114  0.26513    
MINK123M    -1.607e-01  1.449e-01  -1.109  0.26738    
MINKGEM      9.214e-02  9.945e-02   0.927  0.35417    
MKOOPKLA     6.856e-02  4.642e-02   1.477  0.13966    
PWAPART      5.954e-01  3.901e-01   1.526  0.12693    
PWABEDR     -2.757e-01  4.635e-01  -0.595  0.55196    
PWALAND     -4.405e-01  1.035e+00  -0.425  0.67052    
PPERSAUT     2.306e-01  4.199e-02   5.491 4.01e-08 ***
PBESAUT      1.215e+01  4.029e+02   0.030  0.97595    
PMOTSCO     -8.101e-02  1.147e-01  -0.706  0.48006    
PVRAAUT     -2.106e+00  2.557e+03  -0.001  0.99934    
PAANHANG     1.014e+00  9.371e-01   1.082  0.27917    
PTRACTOR     7.229e-01  4.278e-01   1.690  0.09107 .  
PWERKT      -5.525e+00  4.805e+03  -0.001  0.99908    
PBROM        2.170e-01  4.865e-01   0.446  0.65559    
PLEVEN      -2.382e-01  1.170e-01  -2.036  0.04173 *  
PPERSONG    -4.523e-01  2.094e+00  -0.216  0.82901    
PGEZONG      1.444e+00  1.029e+00   1.404  0.16033    
PWAOREG      8.239e-01  5.943e-01   1.386  0.16565    
PBRAND       2.401e-01  7.714e-02   3.113  0.00185 ** 
PZEILPL     -8.658e+00  3.261e+03  -0.003  0.99788    
PPLEZIER    -1.886e-01  3.259e-01  -0.579  0.56289    
PFIETS       3.664e-01  8.325e-01   0.440  0.65985    
PINBOED     -1.068e+00  8.764e-01  -1.219  0.22301    
PBYSTAND    -1.676e-01  3.321e-01  -0.505  0.61373    
AWAPART     -9.293e-01  7.802e-01  -1.191  0.23364    
AWABEDR      4.197e-01  1.082e+00   0.388  0.69824    
AWALAND      2.762e-01  3.528e+00   0.078  0.93758    
APERSAUT    -3.902e-02  1.772e-01  -0.220  0.82566    
ABESAUT     -7.298e+01  2.417e+03  -0.030  0.97591    
AMOTSCO      2.418e-01  3.772e-01   0.641  0.52142    
AVRAAUT     -4.490e+00  1.078e+04   0.000  0.99967    
AAANHANG    -1.351e+00  1.687e+00  -0.801  0.42322    
ATRACTOR    -2.376e+00  1.524e+00  -1.559  0.11899    
AWERKT      -8.749e-01  9.682e+03   0.000  0.99993    
ABROM       -1.060e+00  1.549e+00  -0.684  0.49367    
ALEVEN       4.789e-01  2.245e-01   2.133  0.03291 *  
APERSONG     3.997e-01  4.329e+00   0.092  0.92644    
AGEZONG     -3.163e+00  2.706e+00  -1.169  0.24247    
AWAOREG     -3.212e+00  3.433e+00  -0.936  0.34939    
ABRAND      -4.118e-01  2.787e-01  -1.477  0.13956    
AZEILPL      1.047e+01  3.261e+03   0.003  0.99744    
APLEZIER     2.516e+00  1.010e+00   2.490  0.01276 *  
AFIETS       2.318e-01  5.699e-01   0.407  0.68420    
AINBOED      1.947e+00  1.412e+00   1.378  0.16812    
ABYSTAND     1.078e+00  1.103e+00   0.977  0.32870    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 2635.5  on 5821  degrees of freedom
Residual deviance: 2243.5  on 5736  degrees of freedom
AIC: 2415.5

Number of Fisher Scoring iterations: 17

on a ici un modèle avec beaucoup de variable. Mais si on analyse le summary, on constate que seulement 6 varaibales sont significative.

Regardons un peu le VIF pour toutes les variables.

Show the code 
my_VIFplot(vif(mod1))

On constate la présence de beaucoup de variables avec un VIF très élevé et donc une forte colinéarité indiquant bien qu’il va falloir sélectionner les variables à garder dans notre modèle.

Sélecion automatique

Après toute ces modélisations, rappelons nous tout de même l’objectif de l’assureur est de démarcher des clients de manière ciblée pour leurs faire souscrire une assurance caravane. On pourrait alors de demander : s’il démarchait les clients de façon aléatoire, sans tenir compte de leurs caractéristiques, quel serait environ son taux de réussite ?

Pour cela il suffit juste de ce rappeler du pourcentage donné précédemment qui nous disait la proportion de oui actuellement.

Show the code 
round(table(Caravan$Purchase)*100/nrow(Caravan), 3)

    No    Yes 
94.023  5.977

Le pourcentage étant très bas, on va souhaiter utiliser l’un des 3 modèles estimés ci-dessus (le global, un de ceux sélectionnés par AIC et un de ceux sélectionnés par BIC) pour cibler les clients à démarcher.

Ainsi on regardera

Si l’on choisissait de démarcher tous les clients ayant une probabilité de souscrire l’assurance supérieure à 0.5, quel pourcentage de clients cela représenterait il pour chacun des 3 modèles estimés ? Quel seuil faudrait-il choisir à la place de 0.5 pour que ce pourcentage corresponde à environ 6% des clients ? On décide dans la suite de fixer ce seuil à 0.2 et on cherche à sélectionner le meilleur modèle parmi les 3 précédents.

Conclusion

Session info

Show the code 
sessioninfo::session_info(pkgs = "attached")
─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.4.2 (2024-10-31)
 os       Ubuntu 24.04.1 LTS
 system   x86_64, linux-gnu
 ui       X11
 language (EN)
 collate  fr_FR.UTF-8
 ctype    fr_FR.UTF-8
 tz       Europe/Paris
 date     2025-02-20
 pandoc   3.2 @ /usr/lib/rstudio/resources/app/bin/quarto/bin/tools/x86_64/ (via rmarkdown)

─ Packages ───────────────────────────────────────────────────────────────────
 package   * version date (UTC) lib source
 car       * 3.1-3   2024-09-27 [1] CRAN (R 4.4.2)
 carData   * 3.0-5   2022-01-06 [1] CRAN (R 4.4.2)
 dplyr     * 1.1.4   2023-11-17 [1] CRAN (R 4.4.2)
 ggplot2   * 3.5.1   2024-04-23 [1] CRAN (R 4.4.2)
 gridExtra * 2.3     2017-09-09 [1] CRAN (R 4.4.2)
 ISLR      * 1.4     2021-09-15 [1] CRAN (R 4.4.2)

 [1] /home/clement/R/x86_64-pc-linux-gnu-library/4.4
 [2] /usr/local/lib/R/site-library
 [3] /usr/lib/R/site-library
 [4] /usr/lib/R/library

──────────────────────────────────────────────────────────────────────────────
Show the code 
car <- Caravan
# Question 3 --------------------------------------------------------------

mod_full = glm(car$Purchase~., family = binomial, car)
summary(mod_full)

library(car)
vif(mod_full) # quelques de vif elevé 

## courbe ROC
library(pROC)
library(PresenceAbsence) 
df_rocr_mod = matrix(0, nrow=nrow(as.matrix(car$Purchase)), ncol = 3)
df_rocr_mod[,1] = 1:nrow(as.matrix(car$Purchase))
df_rocr_mod[,2] = as.numeric(mod_full$y)
df_rocr_mod[,3] = mod_full$fitted
df_rocr_mod = as.data.frame(df_rocr_mod)
dimnames(df_rocr_mod)[[2]] = c('ID', "Observed", "Predicted")
dimnames(df_rocr_mod)[[2]]
# matrice de confusion 
cmx(df_rocr_mod, threshold = 0.5)

# Calcul de la specificite et de la sensibilite
sensitivity(cmx(df_rocr_mod,threshold=0.5))
specificity(cmx(df_rocr_mod,threshold=0.5))
# Courbe ROC pour le modele logistique CHD
roc.plot.calculate(df_rocr_mod)
auc.roc.plot(df_rocr_mod) # graphe courbe ROC

auc(df_rocr_mod) # calcul AUC
Show the code 
# Question 4 --------------------------------------------------------------

mod_start = glm(car$Purchase~1, family = binomial, car)

# AIC k = 2 
mod_both_AIC = step(mod_start, scope = formula(mod_full), trace = FALSE, direction = "both", k=2)

# BIC k = log(n)
n = dim(car)[1]
mod_both_BIC = step(mod_start, scope = formula(mod_full), trace = FALSE, direction = "both", k = log(n))

summary(mod_both_AIC)
summary(mod_both_BIC)


vif(mod_both_AIC)
vif(mod_both_BIC)

# on a encore un peu de colinearité pour des var du modèle selec avec AIC
# plus de colinearité pour le model selec avec BIC

# Il serait preferable de garder le mod_both_BIC
#mais on peut aussi enlever les variables au vif elevé 

mod_both_AIC_2.0 = glm(formula = car$Purchase ~ PPERSAUT + MKOOPKLA + PBRAND + APLEZIER + 
                         MOPLLAAG + MBERBOER + MRELGE + PWALAND + AFIETS + MINK123M + 
                         MINKGEM + MGEMLEEF + PWAPART + ABYSTAND + ABRAND + 
                         AWERKT + MGODPR + MSKC + MOPLHOOG + MBERMIDD, family = binomial, 
                       data = car)
summary(mod_both_AIC_2.0)
vif(mod_both_AIC_2.0)

# on analyse tout de même tout les modèle 

#####
# df_rocr_mod_both_AIC
df_rocr_mod_both_AIC = matrix(0, nrow=nrow(as.matrix(car$Purchase)), ncol = 3)
df_rocr_mod_both_AIC[,1] = 1:nrow(as.matrix(car$Purchase))
df_rocr_mod_both_AIC[,2] = as.numeric(mod_both_AIC$y)
df_rocr_mod_both_AIC[,3] = mod_both_AIC$fitted
df_rocr_mod_both_AIC = as.data.frame(df_rocr_mod_both_AIC)
dimnames(df_rocr_mod_both_AIC)[[2]] = c('ID', "Observed", "Predicted")
dimnames(df_rocr_mod_both_AIC)[[2]]
# matrice de confusion 
cmx(df_rocr_mod_both_AIC, threshold = 0.5)

# Calcul de la specificite et de la sensibilite
sensitivity(cmx(df_rocr_mod_both_AIC,threshold=0.5))
specificity(cmx(df_rocr_mod_both_AIC,threshold=0.5))
# Courbe ROC pour le modele logistique CHD
roc.plot.calculate(df_rocr_mod_both_AIC)

# df_rocr_mod_both_AIC_2.0
df_rocr_mod_both_AIC_2.0 = matrix(0, nrow=nrow(as.matrix(car$Purchase)), ncol = 3)
df_rocr_mod_both_AIC_2.0[,1] = 1:nrow(as.matrix(car$Purchase))
df_rocr_mod_both_AIC_2.0[,2] = as.numeric(mod_both_AIC_2.0$y)
df_rocr_mod_both_AIC_2.0[,3] = mod_both_AIC_2.0$fitted
df_rocr_mod_both_AIC_2.0 = as.data.frame(df_rocr_mod_both_AIC_2.0)
dimnames(df_rocr_mod_both_AIC_2.0)[[2]] = c('ID', "Observed", "Predicted")
dimnames(df_rocr_mod_both_AIC_2.0)[[2]]
# matrice de confusion 
cmx(df_rocr_mod_both_AIC_2.0, threshold = 0.5)

# Calcul de la specificite et de la sensibilite
sensitivity(cmx(df_rocr_mod_both_AIC_2.0,threshold=0.5))
specificity(cmx(df_rocr_mod_both_AIC_2.0,threshold=0.5))
# Courbe ROC pour le modele logistique CHD
roc.plot.calculate(df_rocr_mod_both_AIC_2.0)

# df_rocr_mod_both_BIC
df_rocr_mod_both_BIC = matrix(0, nrow=nrow(as.matrix(car$Purchase)), ncol = 3)
df_rocr_mod_both_BIC[,1] = 1:nrow(as.matrix(car$Purchase))
df_rocr_mod_both_BIC[,2] = as.numeric(mod_both_BIC$y)
df_rocr_mod_both_BIC[,3] = mod_both_BIC$fitted
df_rocr_mod_both_BIC = as.data.frame(df_rocr_mod_both_BIC)
dimnames(df_rocr_mod_both_BIC)[[2]] = c('ID', "Observed", "Predicted")
dimnames(df_rocr_mod_both_BIC)[[2]]
# matrice de confusion 
cmx(df_rocr_mod_both_BIC, threshold = 0.5)

# Calcul de la specificite et de la sensibilite
sensitivity(cmx(df_rocr_mod_both_BIC,threshold=0.5))
specificity(cmx(df_rocr_mod_both_BIC,threshold=0.5))
# Courbe ROC pour le modele logistique CHD
roc.plot.calculate(df_rocr_mod_both_BIC)
#####

par(mfrow=c(2,2))
auc.roc.plot(df_rocr_mod, main = "ROC plot mod_full")
auc.roc.plot(df_rocr_mod_both_AIC, main = "ROC plot mod_both_AIC")
auc.roc.plot(df_rocr_mod_both_AIC_2.0, main = "ROC plot mod_both_AIC_2.0")
auc.roc.plot(df_rocr_mod_both_BIC, main = "ROC plot mod_both_BIC") # graphe courbe ROC
par(mfrow=c(1,1))


# On veut maximiser l'AUC, ici les valeurs sont très proche 
# donc on peut quand même préféré le petit modele (BIC) meme si AUC plus faible

## On compare avec anova 

anova(mod_full, mod_both_AIC_2.0)

anova(mod_full, mod_both_BIC)

anova(mod_both_AIC_2.0, mod_both_BIC)
### INTERPRETATION ???????
Show the code 
# Question 5 --------------------------------------------------------------

#demarche aléatoire conduit à 6%
round(table(car$Purchase)*100/n, 3)


# Question 6 --------------------------------------------------------------


mod_full.probs=predict(mod_full, car, type="response")# --> donne les proba
mod_full.pred=rep("No", n)
mod_full.pred[mod_full.probs>.5]="Yes"
table(mod_full.pred, car$Purchase)
# taux de reussitz de démarchage 
# (i.e, le nb de vrais positifs par rapport au nb de positifs prédit)
# 7/(8+7) = 0.4666667
# on arrive à prévoir les souscriptions d'assurances dans 47% des cas
# (8+341)/n = 6% erreur de classification
# (7+5466)/n = 94% precision ou accuracy
# sensibility = 7/(7+341) =0.02
mean(mod_full.pred == car$Purchase) # ne marche pas ??
# = 0

mod_both_AIC_2.0.probs=predict(mod_both_AIC_2.0, car, type="response")# --> donne les proba
mod_both_AIC_2.0.pred=rep("No", n)
mod_both_AIC_2.0.pred[mod_both_AIC_2.0.probs>.5]="Yes"
table(mod_both_AIC_2.0.pred, car$Purchase)
# refaire l'analyse du dessus 

mod_both_BIC.probs=predict(mod_both_BIC, car, type="response")# --> donne les proba
mod_both_BIC.pred=rep("No", n)
mod_both_BIC.pred[mod_both_BIC.probs>.5]="Yes"
table(mod_both_BIC.pred, car$Purchase)
# refaire l'analyse du dessus 



#  % de clients ayant une proba >0.5
round(sum(fitted.values(mod_full)>0.5)*100/n, 3)
# 0.26%
boxplot(fitted.values(mod_full))
quantile(fitted.values(mod_full), 0.94) # seuil pour que ce % corresponde à environ 6% des clients
# 0.1807236 

round(sum(fitted.values(mod_both_AIC_2.0)>0.5)*100/n, 3)
# 0.223
boxplot(fitted.values(mod_both_AIC_2.0))
quantile(fitted.values(mod_both_AIC_2.0), 0.94)
# 0.1759159

round(sum(fitted.values(mod_both_BIC)>0.5)*100/n, 3)
# 0.137
boxplot(fitted.values(mod_both_BIC))
quantile(fitted.values(mod_both_BIC), 0.94)
# 0.1659636 



########
# On décide dans la suite de fixer ce seuil à 0.2 et on cherche à sélectionner 
# le meilleur modèle parmi les 3 précédents.

# on change le seuil
mod_full.pred[mod_full.probs>0.2]=1 # = "Yes"
table(mod_full.pred, car$Purchase)
# taux de reussite demarchage (vrais positifs par rapport au positifs predits)
# 87/(197+87) = 0.306338 = 30.6%

### refaire pour les autres modèles 

mod_both_AIC_2.0.pred[mod_both_AIC_2.0.probs>0.2]=1
table(mod_both_AIC_2.0.pred, car$Purchase)
# 0.2929688

mod_both_BIC.pred[mod_both_BIC.probs>0.2]=1
table(mod_both_BIC.pred, car$Purchase)
# 0.2673797
Show the code 
# Question 7 --------------------------------------------------------------

# Estimer le taux de réussite du démarchage (c’est à dire le nombre de vrais
# positifs par rapport au nombre de positifs prédits) sur 
# l’échantillon d’apprentissage pour chaque modèle

# fct de cout : freq vrai posi parmi les posi preddit
cost = function(r, p){
  # r = reponse
  # p = prevision
  s = sum(p>0.2 & r==1)/sum(p>0.2)
  return(s)
}

cost(mod_full$y, fitted.values(mod_full))
# 0.306338 = 30.6 % 
# on obtient effectivement le même resultat que calculé précédement 

cost(mod_both_AIC_2.0$y, fitted.values(mod_both_AIC_2.0))
#  0.2929688
# ca correspond 

cost(mod_both_BIC$y, fitted.values(mod_both_BIC))
# 0.2673797
# ca correspond 

## Selection  du modele complet
# MAIS les resultats sont trop optimistes car ils sontobtenus via l'echant d'apprent
# Dans ce cas, il n'est pas etonnant que le plus gros mod (mod_full) soit selectionné 
# il faut évaluer l'erreur sur echant test
Show the code 
# Question 8 --------------------------------------------------------------
library(boot)

res = cv.glm(data = car, glmfit = mod_full, cost = cost, K=10)
res2 = cv.glm(car, mod_both_AIC_2.0, cost, K=10)
res3 = cv.glm(car, mod_both_BIC, cost, K=10)
## marche pas. pourquoi??? (voir photo code pour réponse)

res$delta
res2$delta
res3$delta


dim(car)
###### test #####
mod_test = glm(Caravan$Purchase~., family = "binomial", data = Caravan)
cv.glm(Caravan, mod_test, cost = cost, K=10)

summary(Caravan)
Show the code 
# Question 9 --------------------------------------------------------------

# Estimer de même le taux de réussite pour chaque modèle lorsque le seuil
# varie de 0.10 à 0.30 par pas de 0.01


mat=matrix(nrow=3,ncol=21)
k=0
for(s in seq(0.1,0.3,0.01)){
  k=k+1
  cat(k) # Concatenate and Print
  res=cv.glm(Caravan,mod_full,cost,K=10)
  res2=cv.glm(Caravan,mod_both_AIC_2.0,cost,K=10)
  res3=cv.glm(Caravan,mod_both_BIC,cost,K=10)
  mat[1,k]=res$delta[1]
  mat[2,k]=res2$delta[1]
  mat[3,k]=res3$delta[1]
}
matplot(seq(0.1,0.3,0.01),t(mat),type='l')
legend('topleft',c('Tout','AIC','BIC'),col=1:3,lty=1:3)





#repetition 5 fois (tres long)
res_seuil=NULL
for(i in 1:5){
  mat=matrix(nrow=3,ncol=21)
  k=0
  for(s in seq(0.1,0.3,0.01)){
    k=k+1
    cat(k)
    res=cv.glm(Caravan,mod,cost,K=10)
    res2=cv.glm(Caravan,mod2,cost,K=10)
    res3=cv.glm(Caravan,mod3,cost,K=10)
    mat[1,k]=res$delta[1]
    mat[2,k]=res2$delta[1]
    mat[3,k]=res3$delta[1]
  }
  res_seuil[[i]]=mat
}

matplot(seq(0.1,0.3,0.01),t(res_seuil[[1]]),type='l',ylim=c(0.15,0.35),lty=2)
for(i in 2:5) matplot(seq(0.1,0.3,0.01),t(res_seuil[[i]]),type='l',lty=2,add=T)
res_moy=res_seuil[[1]]
for(i in 2:5) res_moy=res_moy+res_seuil[[i]]
matplot(seq(0.1,0.3,0.01),t(res_moy)/5,type='l',lty=1,lwd=2,add=T)
legend('topleft',c('Tout','AIC','BIC'),col=1:3,lty=1:3)

#On observe que les courbes deviennent tres variables lorsque le seuil grandit. Il y a meme des valeurs manquantes
#C'est parcequ'il y a tres peu de positifs predits dans ce cas (voire aucun dans certains folds) et donc l'estimation de l'erreur est tres peu precise
#Le meilleur modele semble celui par BIC. 
#Si on veut avoir a la fois un taux de demarchage optimum et un nombre de positifs pas trop faible, un seuil de 0.2 semble pas mal